Вопросы

- определение основных кинематических характеристик этого движения.

Решение первой задачи сводится к определению необходимого числа функций времени (уравнений движения), однозначно определяющих положение каждой точки тела в пространстве. Решение второй задачи заключается в определении зависимостей, позволяющих по известным уравнениям движения определить траекторию, а также скорость и ускорение любой точки тела в любой момент времени.

Различают пять видов движения твердого тела: поступательное, вращательное, плоскопараллельное, сферическое и свободное. Первые два из них (поступательное и вращательное) называют простейшими.

1. Поступательное движение твердого тела и его свойства.

Докажем следующие свойства поступательного движения. Если тело движется поступательно, то все его точки в каждый момент времени имеют одинаковые скорости и ускорения, а траектории всех точек при наложении совпадают.

Пусть тело движется поступательно. Тогда (см. рис.2.17) для любых двух его точек А и В, в любой момент времени справедливо следующее векторное выражение:

,

где вектор по определению поступательного движения не изменяется ни по величине, ни по направлению. Это означает, что траектории точек А и В смещены относительно друг друга на постоянный вектор и, следовательно, при наложении совпадут.

Рис. 2.17. К определению свойств поступательного движения

Дифференцируя вышеприведенное векторное выражение по времени, получаем:

, или

так как последняя производная (как производная от постоянного вектора ) равна нулю. Дифференцируя равенство скоростей, получаем равенство ускорений:

.

Доказанные свойства позволяют свести изучение поступательного движения тела к изучению движения любой одной из его точек методами кинематики точки.

2. Вращательное движение твердого тела

Движение твердого тела, при котором все точки, лежащие на некоторой прямой, принадлежащей телу или неизменно с ним связанной, остаются неподвижными в рассматриваемой системе отсчета, называется вращательным движением. Упомянутая выше прямая называется осью вращения.

Рис. 2.18. Вращение тела вокруг неподвижной оси

Очевидно, что все точки тела, не лежащие на оси вращения, будут двигаться по окружностям, плоскости которых перпендикулярны оси вращения, а центры лежат на этой оси.

Положение тела при вращательном движении можно однозначно определить углом j между неподвижной полуплоскостью I и подвижной, вращающейся вместе с телом, полуплоскостью II, проходящими через ось вращения. Положительным направлением отсчета угла j, называемого также угловой координатой, принято считать вращение против хода часовой стрелки, если смотреть навстречу оси вращения z . Сам угол j принято измерять в радианах.

Для однозначного определения положения тела в любой момент времени, необходимо располагать зависимостью угловой координаты j от времени:

j = j (t) . (2.25)

Уравнение (2.25) называется уравнением или законом вращательного движения твердого тела.

Введем основные кинематические характеристики вращательного движения - угловую скорость w и угловое ускорение e . Пусть за промежуток времени Dt тело повернется на угол Dj. Тогда отношение Dj / Dt называют средней угловой скоростью за этот промежуток времени: w_ср = Dj / Dt . Предел данного отношения при стремлении Dt к нулю, называют мгновенной или просто угловой скоростью:

. (2.26)

Аналогичным образом вводится понятие углового ускорения:

. (2.27)

Согласно (2.26) и (2.27) угловая скорость и угловое ускорение измеряются в радианах в секунду (рад/с) и в радианах в секунду за секунду (рад/с²) соответственно. Так как радиан является безразмерной величиной, допустимы и более компактные обозначения - (с ^-1) и (с ^-2).

Для того, чтобы использовать угловую скорость и угловое ускорение в векторных выражениях, необходимо рассматривать угловую скорость как вектор, с модулем равным dj/dt и направленным вдоль оси вращения в ту сторону, откуда вращения тела видно происходящим против хода часовой стрелки. Вектор углового ускорения, модуль которого равен dw/dt, также считают направленным вдоль оси вращения. Он совпадает по направлению с вектором угловой скорости при ускоренном вращении и противоположен ему при замедленном вращении тела (рис. 2.19). Необходимо отметить, что введенные таким необычным способом векторы называют псевдовекторами ( как бы векторами), чтобы подчеркнуть их некоторую “векторную неполноценность”. Тем не менее теперь становится возможна запись следующей векторной формулы:

, (2.28)

правильно отражающей не только количественную связь и , но и взаимосвязь направлений векторов и , отображенной на рисунке 2.19.

Рис. 2.19. Взаимосвязь направлений ц и e

а) Равномерное вращение - вращение с постоянной угловой скоростью

(w = const):

, , .

Пусть при t = 0: j = 0, тогда С = 0 и мы получаем следующее уравнение или закон равномерного вращения:

. (2.33)

в) Равнопеременное вращение - это вращение с постоянным угловым ускорением (e = const):

, , ,

, ,

.

Пусть при t = 0: w = w₀ и j₀ = 0, тогда С₁ = w₀ , C₂ = 0. Подставляя найденные значения констант интегрирования в полученные выше выражения, получаем:

, (2.34)

. (2.35)

В полученном законе изменения угловой скорости (2.34) и в уравнении равнопеременного вращения (2.35), угловое ускорение e будет положительным при равноускоренном вращении и отрицательным при равнозамедленным.

В заключение приведем вполне очевидные соотношения, которые часто используются при решении задач:

, (2.36)

где N - число оборотов, n - угловая скорость в оборотах в минуту.

4.Формула Эйлера

В заключение получим векторные формулы для скорости и ускорения точек в круговом движении. Рассмотри движение точки М, не лежащей на оси вращения (рис. 2.22). Покажем, что ее скорость полностью определяется формулой Эйлера : . (2.37)

Рис. 2.22. Иллюстрация формулы Эйлера

Действительно, модуль векторного произведения равен V=w r sina= = w R, что совпадает с выражением (2.29). Формула (2.34) правильно определяет и направление вектора скорости: вектор 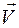направлен перпендикулярно плоскости треугольника ОСМ в ту сторону, откуда поворот от к 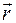виден происходящим против хода часовой стрелки (т.е. вектор 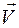направлен, как и полагается, по касательной к траектории в направлении вращения тела).

Для вывода векторных формул, определяющих ускорение, продифференцируем формулу Эйлера по времени:

.

Учитывая, что согласно (2.28) и (2.5)

,

получаем:

, (2.38)

где , . (2.39)

В справедливости выражений (2.36) можно убедиться непосредственно, определив модули и направления входящих в них векторных произведений. Так согласно первой формуле (2.39) , что совпадает с уже известным выражением (2.30). Правильно определяется и направление вектора (см. рис.2.22). Вторая формула (2.39) дает [сравните с (2.31)]. Направлен вектор , как и положено, перпендикулярно плоскости, в которой лежат перемножаемы векторы внутрь траектории, откуда поворот от к вектору виден происходящим против хода часовой стрелки.