Лекция 13
Рис. 2.13. Определение кривизны кривой
Средней кривизной на этом участке траектории называется отношение kср = Dj / DS. Предел этого отношения при D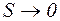 называется кривизной траектории в точке M, а величина обратная кривизне, называется радиусом кривизны.
называется кривизной траектории в точке M, а величина обратная кривизне, называется радиусом кривизны.
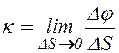 . (2.15)
. (2.15) 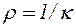 (2.16)
(2.16)
Вычислим производную единичного вектора  по времени -
по времени -  . Для определения модуля производной отложим из одного центра векторы
. Для определения модуля производной отложим из одного центра векторы  и
и  (рис. 2.14). Учитывая, что изменение единичного вектора
(рис. 2.14). Учитывая, что изменение единичного вектора  ‚ равно основанию образовавшегося равнобедренного треугольника, получаем:
‚ равно основанию образовавшегося равнобедренного треугольника, получаем:

Рис. 2.14. К определению величины и направления вектораdт/dt


Из рис. 2.14 видно, что при стремлении Dt к нулю, углы при основании треугольника стремятся к прямым углам и, следовательно, вектор  направлен перпендикулярно вектору
направлен перпендикулярно вектору  ‚ внутрь траектории (т.е. по главной нормали). С учетом этого:
‚ внутрь траектории (т.е. по главной нормали). С учетом этого:
 . (2.17)
. (2.17)
Перейдем к выводу формул, определяющих ускорение точки при естественном способе задания движения. Согласно (2.10) и (2.11), имеем:
 . (2.18)
. (2.18)
Первое слагаемое в правой части (2.18) направлено по касательной к траектории и называется касательной составляющей полного ускорения:
 ,
,  . (2.19)
. (2.19)
Если  ,то касательное ускорение
,то касательное ускорение  направлено в сторону увеличения дуговой координаты S (т.е. совпадает по направлению с вектором
направлено в сторону увеличения дуговой координаты S (т.е. совпадает по направлению с вектором 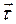 ). Второе слагаемое в правой части выражения (2.18) называется нормальной составляющей полного ускорения , так как согласно (2.15), (2.16) и (2.17):
). Второе слагаемое в правой части выражения (2.18) называется нормальной составляющей полного ускорения , так как согласно (2.15), (2.16) и (2.17):
 ,
,
 ,
,  . (2.20)
. (2.20)
Итак, ускорение при естественном способе задания движения определяется как геометрическая сумма (рис. 2.15) его касательной и нормальной составляющих:
 ,
,  . (2.21)
. (2.21)

Рис. 2.15. Определение полного ускорения точки
Касательное ускорение характеризует изменение скорости по величине, нормальное ускорение - по направлению. Отметим случаи, когда равны нулю отдельные составляющие ускорения.
Касательное ускорение Wt = dV/dt равно нулю при равномерном движении ( V = const) и в точках траектории, где величина скорости достигает своего минимального или максимального значения (dV/dt)=0.
Нормальное ускорение Wn = V2/r равно нулю при прямолинейном движении и в точках перегиба траектории (когда  ), а также в моменты смены направления скорости на противоположное (когда V = 0).
), а также в моменты смены направления скорости на противоположное (когда V = 0).
2.Частные случаи движения точки
Все выведенные выше формулы справедливы для любого движения точки. Рассмотрим теперь два важных частных случая - равномерное и равнопеременное движение.
Равномерным называется движение точки с постоянной по величине скоростью, т.е. когда V = const. Выведем уравнение равномерного движения.
Согласно (2.10) V = dS/dt или dS = V dt. Интегрируя последнее выражение и учитывая, что V = const, получаем закон равномерного движения:
 . (2.22)
. (2.22)
Равнопеременным (равноускоренным или равнозамедленным) называется движение с постоянным по величине касательным ускорением (Wt= const). Получим формулы для такого движения. Имеем:
 ,
,  ,
,  ,
,
 - закон изменения скорости. (2.23)
- закон изменения скорости. (2.23)
Подставляя вместо V = dS/dt и интегрируя полученное выражение, находим закон или уравнение равнопеременного движения:
 ,
,  ,
,  ,
,
 . (2.24)
. (2.24)
Пример.Точка движется по окружности радиуса R равноускоренно из состояния покоя и совершает первый полный оборот за T секунд. Определить модули скорости и ускорения точки в конце этого промежутка времени.
Решение. Так как по условию задачи движение точки равноускоренное, воспользуемся формулой (2.24) для определения касательного ускорения точки:
 .
.
Подставляя S = 2p R, t = T и V0 = 0 , определяем Wt:
 .
.
Зная Wt , определяем скорость точки в момент времени T по формуле (2.23):
 .
.
Нормальное ускорение точки в момент времени T будет равно
 .
.
Полное ускорение точки определяем по формулу (2.21):
 .
.