Вопросы

Рис. 2.2. Вид траектории точки в примере 1

 

Пример 2.

Движение точки в плоскости xOy описывается уравнениями:

x = 3 sin 4t , y = 4 cos 4t .

Найти уравнение траектории в координатной форме.

Решение: Перепишем исходные уравнения движения в виде:

x/3 = sin4t , y/4 = cos4t

возводя оба уравнения в квадрат и складывая их почленно, получим уравнение траектории в координатной форме: .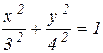

 

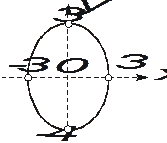
Рис. 2.3. Вид траектории движения точки в примере 2

 

в) Естественный способ задания движения точки.

Рассмотрим естественный способ задания движения точки, когда отдельно задается:

-траектория движения;

-начало и положительное направление отсчета;

-закон движения точки по траектории:S = S(t),

где S - дуговая координата (расстояние, измеренное от выбранного на траектории начала отсчета до текущего положение точки на траектории).

 

Рис. 2.4. Естественный способ движения точки

 

Поскольку одно и то же движение точки может задаваться тремя различными способами, между ними должна существовать связь и от одного способа задания можно переходить к другому. Такой переход от векторного способа к координатному и наоборот очевиден (формулы 2.2, 2.3). Рассмотрим пример перехода от естественного способа задания движения к координатному:

Пусть точка движется по окружности x² + y² = a² по закону S = Vt, где a и V заданные константы (рис. 2.5). Начало отсчета - точка М(а,0). Положительное направление отсчета координаты S - против хода часовой стрелки. Определить уравнения движения точки в координатной форме: x = x(t), y = y(t).

 

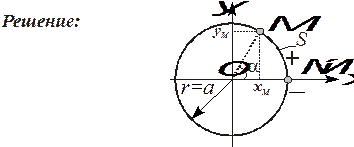
Рис. 2.5. Траектория, начало отсчета и положительное направление движения

 

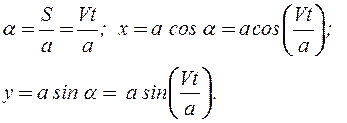
Для обратного перехода к естественному способу задания движения нужно исключив время t из полученных уравнений движения, получить уравнение траектории , а затем по формуле 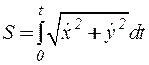и закон движения точки по траектории: .

 

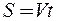Лекция 11