Кинематика точки

Способы задания движения точки

Основные задачи кинематики

Основные понятия

Вопросы

 

1. Кинематикой называется раздел теоретической механики, в котором изучаются геометрические свойства механического движение тел, без учета их масс и действующих на них сил.

Под механическим движением понимается изменение с течением времени положение тела в пространстве по отношению к другим телам. Для того чтобы определить изменение положения тела по отношению к другому телу, с последним связывают какую-либо систему координатных осей, называемую системой отсчета. В зависимости от тела, с которым она связана, система отсчета может быть как подвижной, так и неподвижной. Тело движется по отношению к выбранной системой отсчета, если с течением времени изменяются координаты хотя бы одной из его точек; в противном случае тело по отношению к данной системе отсчета будет находиться в состоянии покоя. Таким образом, покой и движение - понятия относительные, зависящие от выбора системы отсчета.

Механическое движение происходит в пространстве и во времени. При этом пространство считается трехмерным евклидовым пространством. Все измерения в нем производятся на основании методов евклидовой геометрии. За единицу длины при измерении расстояния принят 1 метр. Время в механике считается универсальным, т.е. протекающем одинаково во всех системах отсчета. За единицу времени принимается 1 секунда.

В задачах кинематики время t принимается за независимое переменное (аргумент). Все другие переменные величины (расстояние, скорость, ускорение и т.д. ) рассматриваются как функции времени t. Отсчет времени ведется от некоторого начального момента (t = 0), о выборе которого в каждом случае уславливаются. Всякий данный момент времени t определяется числом секунд, прошедшим от начального момента; разность между какими-нибудь двумя моментами времени называется промежутком времени.

Для решения задач кинематики необходимо, чтобы изучаемое движение было как-то задано (описано). Движение тела считается заданным, если известно положение всех его точек (относительно выбранной системы отсчета) в любой момент времени.

 

2.Две основные задачи кинематики

Основными задачами кинематики являются:

а) установление математических способов задания движения тел в произвольно выбранной системе отсчета,

б) определение по заданному движению тела всех основных кинематических характеристик (траектории, скорости, ускорения) любой из его точек. Рассмотрим решение этих задач для одной точки.

 

 

3. Способы задания движения точки

Для задания движения в кинематике используются три способа: векторный, координатный и естественный.

а) Векторный способ задания движения точки.

Пусть точка М движется по некоторой кривой АВ. Положение точки M относительно начала некоторой системы координат можно однозначно определить с помощью радиус-вектора 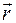, начало которого неизменно связано с точкой О. Движение точки М будет полностью определено, если ее радиус вектор задан как функция времени. Векторное равенство:

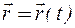(2.1)

называется векторным уравнением движения или законом движения точки в векторной форме.

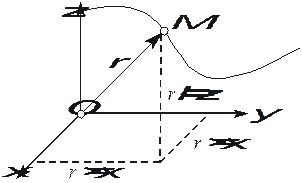
Рис. 2.1. Векторный способ задания движения точки

 

При движении точки М длина и ориентация вектора 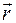будет меняться, а его конец будет вычерчивать в пространстве линию называемую годографом радиуса - вектора 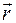или траекторией движения точки М (рис. 2.1).

Выражая в (1) вектор 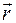через его проекции 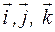, получим:

,

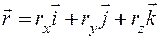или учитывая, что проекции радиуса-вектора равны координатам точки М:

r_x = x, r_y = y, r_z = z,

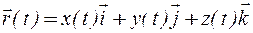, (2.2)

где x(t), y(t), z(t) - текущие координаты движущейся точки М.

 

б) Координатный способ задания движения точки.

С векторным способом тесно связан координатный способ задания движения точки. Очевидно, что положение движущейся точки в пространстве будет однозначно определено, если будут известны текущие координаты точки, фигурирующие в выражении (1.2):

x = x(t), y = y(t), z = z(t). (2.3)

Уравнения (2.3) называются уравнениями движения или законом движения точки в координатной форме. Эти же уравнения можно трактовать как параметрические уравнения траектории, в которых роль параметра играет время t. Чтобы получить уравнение траектории в координатной форме, нужно из уравнений (3) исключить время t.

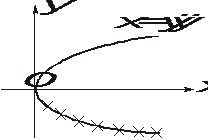
Пример 1.

Пусть движение точки задано уравнениями:

x = t², y = t,

где t измеряется в секундах, x и y в метрах. Определить уравнение траектории.

Исключая из уравнений движения t, получим уравнение траектории

t = y, x = y².

 

Поскольку время t >0, координата y в исходных уравнениях движения не может быть отрицательной. Следовательно, траекторией движения будет лишь верхняя ветвь параболы x = y² .