Вектор ускорения точки в данный момент времени равен первой производной от вектора скорости или второй производной от её радиуса-вектора по времени.

Вектор скорости точки в данный момент времени равен первой производной от её радиуса-вектора по времени. Вектор скорости направлен по касательной к траектории данной точки в сторону движения.

Ускорение точки в векторной форме.

 

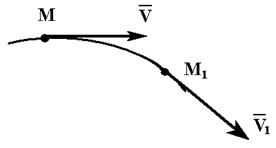
Пусть точка движется по криволинейной траектории. В момент времени

,

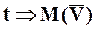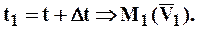
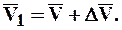
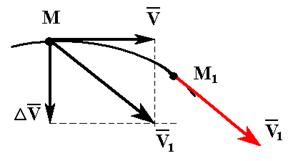
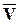Перенесём вектор параллельно самому себе в точку М и построим параллелограмм, у которого сторона , а диагональ . Тогда, очевидно, что другой стороной будет DV.

Отношение приращения вектора скорости к тому промежутку времени, за который это приращение произошло, называется вектором среднего ускорения. Направление такое же, как у .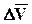

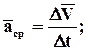
Ускорение в данный момент времени равно пределу

 

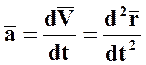
Если точка движется по прямолинейной траектории, то вектор ускорения направлен по этой прямой.

Если точка движется по криволинейной траектории (плоской), то вектор ускорения направлен в сторону вогнутости кривой.

 

1.2. Координатный способ задания движения точки.

Положение точки в пространстве и на траектории однозначно определяется тремя координатами x, y, z.

При движении точки координаты будут меняться в зависимости от времени.

 

x = f₁ (t)

y = f₂ (t) - закон движения точки

z = f₃ (t) в координатной форме.

 

 

Определение траектории точки.

Если t принять за параметр в уравнениях, выражающих закон движения, то эти уравнения будут представлять собой уравнения траектории в параметрической форме. Чтобы получить уравнение траектории в координатной форме надо исключить параметр t .

 

Пример:

x = 2 t

y = 4 t² – 1

t₁ = 1 c.

________________

x = ¦(y)

 

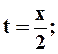
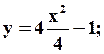
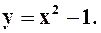
Траектория – парабола:

 

Определение скорости точки при координатном способе задания

её движения.

 

 

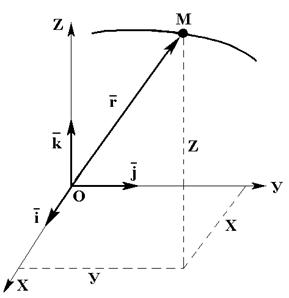Положение точки на траектории одно-

значно определяется радиус-вектором

или тремя декартовыми координатами.

Координаты можно рассматривать как

проекции данного радиуса-вектора на

оси. Построим единичные векторы дан-

ной системы – Разложим радиус-вектор по осям координат:

 

 

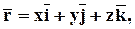
Определяем скорость точки как производную от радиуса-вектора .

 

 

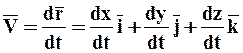
- const, так как система осей неподвижна.

 

Разложим вектор по осям координат:

 

 

Учитывая, что вектор может быть разложен единственным образом по данным осям, приравниваем коэффициенты при одинаковых ортах.

 

 

 

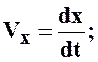
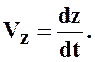
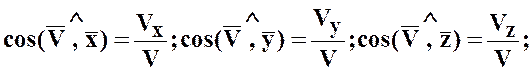
Определение ускорения точки.

Аналогично определяем ускорение точки.

 

 

 

 

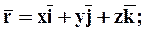
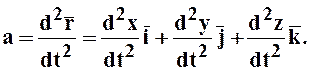
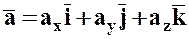
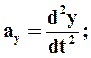
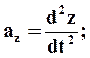
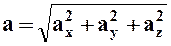
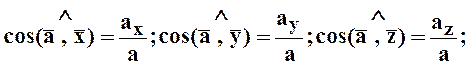
Пример:

Дано: x = 2t см; y =4t² – 1 см t₁ = 1c.

Найти: V_x; V_y; V_a;

 

V_x = x^/ = (2t)^/ = 2^.1 =2 см/с

 

V_y = y^/ = (4t² -1)^/ = 4^.2^.t -0 = 8t см/c

 

см/с

a_x = х^// = 0 см/с²

a_y = y^// = 8 см/с²

 

 

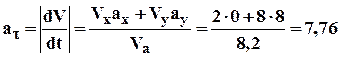см/с²

 

см/с²

см

1.3. Естественный способ задания движения точки.

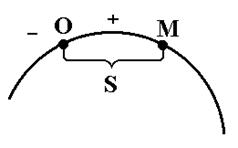
Чтобы задать движение точки естественным

способом необходимо:

- знать траекторию движения;

- знать начало отсчёта и + и – направление

отсчёта;

- знать закон движения точки по траектории в виде S = f (t); S– криволинейная координата.

 

Определение скорости точки.

 

 

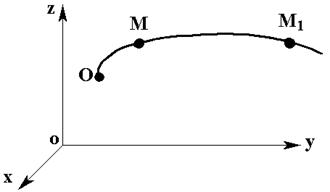
Точка движется по криволинейной траектории.

В момент t – M (S),

t₁ = t + Dt – M₁(S₁);

S₁ = S + DS.

 

 

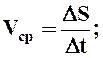
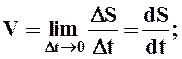
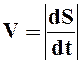
Скорость при естественном способе задания движения равна первой производной от криволинейной координаты движения точки по времени. Знак производной указывает направление вектора скорости.

 

Кривизна и радиус кривизны.

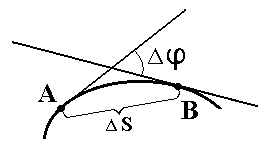
Возьмём на некоторой кривой две точки А и В.

Проведём через эти точки касательные. Угол между этими касательными называется углом смежности Δφ.