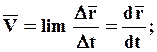КИНЕМАТИКА
РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА
Лектор: ст. преподаватель Какурина Светлана Константиновна
КУРС ЛЕКЦИЙ
Министерство образования Российской Федерации
Государственное образовательное учреждение
высшего профессионального образования
«Государственный Университет цветных металлов и золота»
Кафедра: «ТЕХНИЧЕСКАЯ МЕХАНИКА»
По дисциплине: «ТЕОРЕТИЧЕСКАЯ МЕХАНИКА»
Раздел: «КИНЕМАТИКА»
Для студентов всех специальностей
дневного и заочного обучения
Красноярск 2012г.
1. Яблонский А.А., Никифорова В.М. Я 14 Курс теоретической механики. Учебник для техн. вузов. – 7-е изд. стереотипное. – Серия «Учебники для вузов. Специальная литература». – СПб.: Издательство «Лань», 1999. – 768 с.
2. Тарг С.М. Курс теоретической механики. М., 1963 и последующие издания.
3. Бать М.И., Джанелидзе Г.Ю., Кельзон А.С. Теоретическая механика в примерах и задачах, ч. I и II. М., 1961 и последующие издания.
4. Сборник заданий для курсовых работ по теоретической механике / Под ред. проф. А.А. Яблонского. М., 1968 и последующие издания.
Кинематика – раздел теоретической механики, в котором изучается движение тел без учёта сил, вызывающих движение, то есть без учёта сил приложенных к движущимся телам.
1. Кинематика точки.
Точка, двигаясь в пространстве, описывает некоторую линию. Линия, представляющая геометрическое место последовательных положений точки, называется траекторией этой точки. По виду траектории делятся на прямолинейные и криволинейные. Изучить кинематику движущейся точки, значит определить её траекторию за данный промежуток времени и определить скорость и ускорение её в каждый момент времени.
Закон движения точки может быть задан тремя способами:
- векторный;
- координатный;
- естественный.
1.1. Векторный способ задания движения точки.
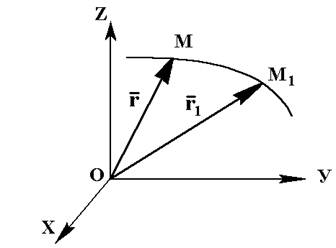
Пусть материальная точка М движется по криволинейной траектории относительно системы осей координат OXYZ. Положение точки на траектории однозначно определяется её радиусом-вектором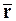 
.
При движении точки радиус-вектор будет меняться по величине и по направлению. 
– закон движения точки
в векторной форме.
Линия, представляющая геометрическое место концов переменного вектора, начало которого находится в определённой точке пространства, называется годографом этого вектора. Траектория движения точки является годографом её радиуса-вектора.
Уравнение скорости точки в векторной форме.
Пусть точка движется по криволинейной траектории относительно системы осей координат OXYZ. В момент времени t точка занимает положение М, t1 = t +Δt → М1. Вектор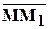 
, начало которого находится в начальном положении точки, а конец в конечном положении точки, называется вектором перемещения точки.
Отношение вектора перемещения к тому промежутку времени, за который произошло это перемещение, называется вектором средней скорости точки.
 | |||
 |
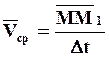
Так как Dt скалярная положительная
величина, то вектор 
направлен так же как вектор 
. Скорость точки в данный момент времени равна:
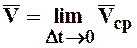
Из треугольника ОММ1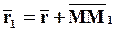 
,
отсюда: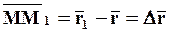 
.
Тогда: 
