Пара вращений
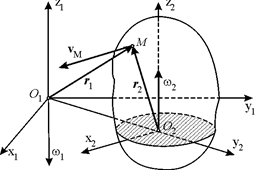 Рис. 8.5.
Рис. 8.5.
| Рассмотрим сложное движение, состоящее из двух вращений относительно параллельных осей О1z1 и О2z2 (рис. 8.5). Пусть угловые скорости относительного (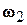 ) и переносного ( ) и переносного (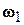 ) движений равны по модулю, но противоположно направлены ( ) движений равны по модулю, но противоположно направлены (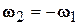 ). Такая совокупность движений называется парой вращений. ). Такая совокупность движений называется парой вращений.
|
Найдем абсолютную скорость какой-либо точки М твердого тела:
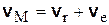 .
.
В нашем случае
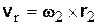 ,
, 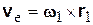 ,
,
следовательно,
 (8.9)
(8.9)
Векторы 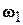 и
и 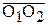 не зависят от положения точки М, поэтому из (8.9) вытекает, что скорости всех точек тела одинаковы. Этим свойством обладает только поступательное движение.
не зависят от положения точки М, поэтому из (8.9) вытекает, что скорости всех точек тела одинаковы. Этим свойством обладает только поступательное движение.
Из (8.9) следует, что
 (8.10)
(8.10)
Векторное произведение 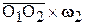 называется моментом пары вращений. Таким образом, тело, участвующее в паре вращений, движется поступательно со скоростью, равной моменту пары вращений. Легко видеть, что совокупность
называется моментом пары вращений. Таким образом, тело, участвующее в паре вращений, движется поступательно со скоростью, равной моменту пары вращений. Легко видеть, что совокупность 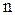 пар вращений эквивалентна одной паре, т.е. поступательному движению. Заметим, что любое мгновенно-поступательное движение можно представить как мгновенную пару вращений.
пар вращений эквивалентна одной паре, т.е. поступательному движению. Заметим, что любое мгновенно-поступательное движение можно представить как мгновенную пару вращений.