Сложение поступательных движений
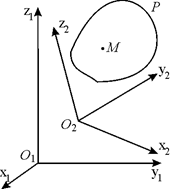 Рис. 8.1.
Рис. 8.1.
| Пусть 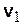 – скорость поступательного движения тела Р относительно системы О2x2y2z2 (рис. 8.1), a – скорость поступательного движения тела Р относительно системы О2x2y2z2 (рис. 8.1), a 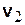 – скорость поступательного движения системы О2x2y2z2 относительно неподвижной системы координат О1x1y1z1. Тогда, чтобы найти абсолютную скорость какой-либо точки М тела Р, нужно применить теорему о сложении скоростей: – скорость поступательного движения системы О2x2y2z2 относительно неподвижной системы координат О1x1y1z1. Тогда, чтобы найти абсолютную скорость какой-либо точки М тела Р, нужно применить теорему о сложении скоростей:
|
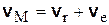 . (8.1)
. (8.1)
В нашем случае 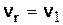 и
и 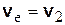 следовательно,
следовательно,
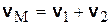 . (8.2)
. (8.2)
Таким образом, у всех точек тела абсолютные скорости оказались одинаковыми, следовательно, при сложении поступательных движений твердого тела результирующее движение будет также поступательным и скорость результирующего движения равна сумме скоростей составляющих движений.
В случае 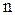 поступательных движений, применяя последовательно формулу (8.1), можно показать, что результирующее движение также будет поступательным и его скорость будет равна сумме скоростей составляющих движений, т.е.
поступательных движений, применяя последовательно формулу (8.1), можно показать, что результирующее движение также будет поступательным и его скорость будет равна сумме скоростей составляющих движений, т.е.
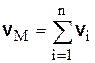 .
.
Возможен случай, когда скорости всех точек тела только в данный момент времени оказываются равными между собой. Этот случай называют мгновенно-поступательным движением. Однако следует иметь в виду, что ускорения точек при этом различны.
8.3. Сложение вращений вокруг пересекающихся осей.
Кинематические уравнения Эйлера
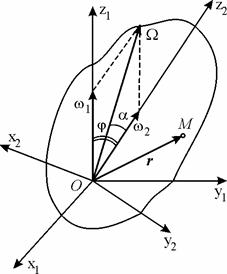 Рис. 8.2.
Рис. 8.2.
| Пусть тело Р вращается в системе координат Оx2y2z2 вокруг оси z2 с угловой скоростью 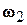 , а система координат Оx2y2z2 вращается вокруг оси z1 неподвижной системы с угловой скоростью , а система координат Оx2y2z2 вращается вокруг оси z1 неподвижной системы с угловой скоростью 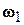 (рис. 8.2). Точка О остается неподвижной, поэтому результирующее движение тела будет сферическим. Обозначим через (рис. 8.2). Точка О остается неподвижной, поэтому результирующее движение тела будет сферическим. Обозначим через 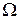 угловую скорость этого движения. Наша задача состоит в том, чтобы угловую скорость этого движения. Наша задача состоит в том, чтобы
|
найти угловую скорость абсолютного движения тела, зная угловые скорости 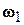 и
и 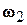 составляющих вращений.
составляющих вращений.
Найдем абсолютную скорость произвольной точки М тела. Для этого в формулу (8.1) следует подставить
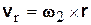 ,
, 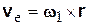 ,
,
где 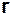 – радиус-вектор точки М; тогда
– радиус-вектор точки М; тогда
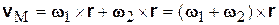 .
.
С другой стороны, скорость той же точки М в абсолютном движении будет равна
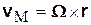 .
.
Сравнивая оба равенства, получим
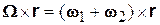 .
.
Так как точка М, а следовательно, и ее радиус-вектор 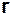 произвольны, то
произвольны, то
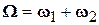 . (8.3)
. (8.3)
Из формулы (8.3) следует, что совокупность двух вращений, происходящих вокруг пересекающихся осей, эквивалентна одному вращению, происходящему с мгновенной угловой скоростью, равной сумме угловых скоростей составляющих вращений.
Замечание. В случае 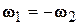 из (8.3) следует, что
из (8.3) следует, что 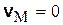 . Следовательно, совокупность двух вращений вокруг одной и той же оси, происходящих с одинаковыми по модулю, но противоположно направленными угловыми скоростями, эквивалентна покою. Такую совокупность движений всегда можно присоединять к любому сложному движению тела.
. Следовательно, совокупность двух вращений вокруг одной и той же оси, происходящих с одинаковыми по модулю, но противоположно направленными угловыми скоростями, эквивалентна покою. Такую совокупность движений всегда можно присоединять к любому сложному движению тела.
Совокупность 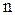 вращений вокруг пересекающихся в одной точке осей эквивалентна одному вращению с мгновенной угловой скоростью
вращений вокруг пересекающихся в одной точке осей эквивалентна одному вращению с мгновенной угловой скоростью
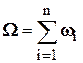 .
.
Полученное правило сложения вращений вокруг пересекающихся осей позволит нам теперь выразить проекции мгновенной угловой скорости тела, имеющего одну неподвижную точку О, через углы Эйлера и их производные.
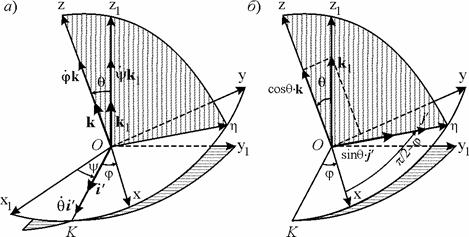 Рис. 8.3.
Рис. 8.3.
|
Напомним, что положение подвижной системы координат Oxyz, жестко связанной с телом, полностью определяется относительно неподвижной системы координат Оx1y1z1 углами Эйлера (рис. 8.3). Тело участвует в трех вращениях: первое вращение, соответствующее изменению угла прецессии  , происходит вокруг неподвижной оси Оz1 с угловой скоростью
, происходит вокруг неподвижной оси Оz1 с угловой скоростью 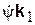 ; второе вращение, соответствующее изменению угла нутации
; второе вращение, соответствующее изменению угла нутации  , происходит вокруг линии узлов ОК с угловой скоростью
, происходит вокруг линии узлов ОК с угловой скоростью 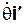 , где
, где  – единичный вектор линии узлов; наконец, третье вращение, соответствующее изменению угла собственного вращения
– единичный вектор линии узлов; наконец, третье вращение, соответствующее изменению угла собственного вращения 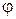 , происходит вокруг оси Oz с угловой скоростью
, происходит вокруг оси Oz с угловой скоростью 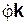 . Следовательно, абсолютная угловая скорость
. Следовательно, абсолютная угловая скорость  тела будет
тела будет
 , (8.4)
, (8.4)
Составим таблицу направляющих косинусов единичных векторов 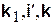 в системе подвижных осей Oxyz:
в системе подвижных осей Oxyz:
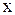
| 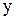
| 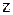
| |
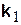
| 
| 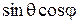
| 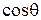
|
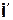
| 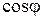
| 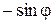
| |
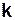
|
Поясним составление первой строки этой таблицы (вторая и третья строки непосредственно следуют из рис. 8.3 а). Разложим единичный вектор 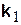 на две взаимно перпендикулярные составляющие, направив одну из них по оси z (она равна
на две взаимно перпендикулярные составляющие, направив одну из них по оси z (она равна 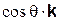 , см. рис. 8.3 б); тогда вторая составляющая, равная
, см. рис. 8.3 б); тогда вторая составляющая, равная 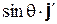 , где
, где 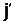 – единичный вектор вспомогательной оси
– единичный вектор вспомогательной оси 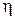 , будет находиться в плоскости ху. Следовательно,
, будет находиться в плоскости ху. Следовательно,
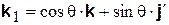 . (8.5)
. (8.5)
Вспомогательная ось 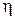 составляет с осями х и у углы
составляет с осями х и у углы 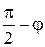 и
и 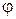 . Проектируя единичный вектор
. Проектируя единичный вектор 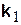 на оси х, у и z, получим (напомним, что проекции единичных векторов равны соответствующим направляющим косинусам)
на оси х, у и z, получим (напомним, что проекции единичных векторов равны соответствующим направляющим косинусам)
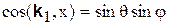 ,
, 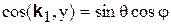 ,
,  .
.
Эти выражения и составляют первую строку таблицы направляющих косинусов.
Проектируя теперь обе части равенства (8.4) на оси х, у и z и учитывая таблицу косинусов, найдем проекции вектора угловой скорости тела на оси, жестко связанные с телом:
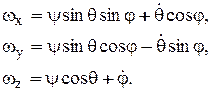 (8.6)
(8.6)
Полученные соотношения носят название кинематических уравнений Эйлера.
Модуль угловой скорости определяется равенством
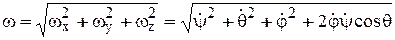 . (8.7)
. (8.7)
Таблица направляющих косинусов между единичными векторами 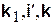 в системе неподвижных осей Оx1y1z1 имеет вид
в системе неподвижных осей Оx1y1z1 имеет вид
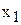
| 
| 
| |
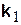
| |||
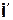
| 
| 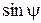
| |
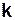
| 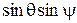
| 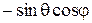
| 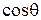
|
Для того чтобы получить последнюю строку, мы разложили вектор 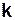 на две составляющие, направив одну из них по оси
на две составляющие, направив одну из них по оси  (она равна
(она равна 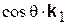 ; см. рис. 8.4); тогда вторая, равная
; см. рис. 8.4); тогда вторая, равная 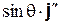 , где
, где 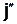 – единичный вектор новой вспомогательной оси
– единичный вектор новой вспомогательной оси 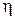 , будет находиться в плоскости Оx1y1:
, будет находиться в плоскости Оx1y1:
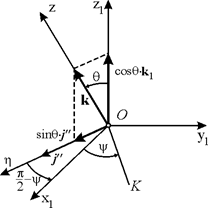 Рис. 8.4.
Рис. 8.4.
| 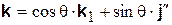 .
Третья строка второй таблицы получена проектированием этого равенства на оси .
Третья строка второй таблицы получена проектированием этого равенства на оси 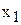 , ,  , ,  и пользуясь второй таблицей направляющих косинусов, найдем проекции вектора угловой скорости на неподвижные оси координат: и пользуясь второй таблицей направляющих косинусов, найдем проекции вектора угловой скорости на неподвижные оси координат:
|
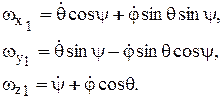 (8.8)
(8.8)
Кинематические уравнения Эйлера (8.6) и (8.8) устанавливают связь между проекциями вектора угловой скорости  на соответствующие оси, углами Эйлера
на соответствующие оси, углами Эйлера 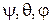 и их первыми производными по времени.
и их первыми производными по времени.