Теорема о сложении скоростей

 

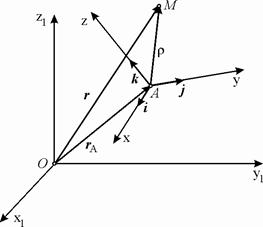Рис. 7.1.

Выбирая систему координат Oxly1z1 за основную, предположим, что система координат Ахуz движется по отношению к основной системе произвольным образом (рис. 7.1). Скорость произвольной точки М по отношению к основной системе координат называется абсолютной скоростью.

Скорость 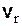точки по отношению к подвижной системе координат называется относительной скоростью. Переносной скоростью 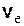точки называется скорость той точки подвижной системы координат, с которой в данный момент совпадает движущаяся точка.

Если радиус-вектор определяет положение точки М по отношению к системе координат Ох₁у₁z₁, радиус-вектор определяет положение начала системы координат Ахуz в системе Ох₁у₁z₁, а радиус-вектор 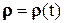определяет положение точки М в системе координат Ахуz, то в соответствии с рис. 7.1 имеем

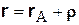. (7.6)

Пусть координаты точки в подвижной системе координат будут х, у и z; тогда ,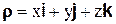

где i, j, k – единичные векторы осей подвижной системы координат.

По определению абсолютная производная радиуса-вектора по времени будет абсолютной скоростью точки. Следовательно, дифференцируя равенство (7.6) по времени, найдем абсолютную скорость точки

. (7.7)

Так как вектор определен в подвижной системе координат, то для нахождения абсолютной производной от него воспользуемся формулой (7.5):

, (7.8)

где – угловая скорость подвижной системы координат, а

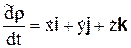
представляет собой относительную производную от по времени. Согласно определению это будет относительная скорость точки, т.е.

. (7.9)

Подставляя выражения (7.8) и (7.9) в соотношение (7.7), получим

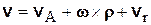, (7.10)

где – скорость начала подвижной системы координат по отношению к основной.

Для определения переносной скорости точки закрепим ее в подвижной системе координат, т.е. положим в формуле (7.10) , тогда получим

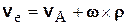. (7.11)

Таким образом, имеем

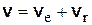, (7.12)

т. е. абсолютная скорость точки равна геометрической сумме переносной и относительной скоростей.