Абсолютная и относительная производные от вектора

Основные определения.

СЛОЖНОЕ ДВИЖЕНИЕ ТОЧКИ

Геометрической сумме ускорения полюса и ускорения этой точки в ее движении вокруг полюса.

 

В некоторых случаях целесообразно изучать движение точки одновременно по отношению к двум системам координат, одна из которых совершает заданное движение по отношению к другой (основной), принимаемой за неподвижную.

Будем называть сложным или «абсолютным» движением точки ее движение по отношению к системе координат, выбранной за основную. Движение точки по отношению к подвижной системе координат будем называть относительным. Под переносным движением будем понимать движение подвижной системы координат относительно неподвижной.

Далее мы встретимся с необходимостью дифференцирования вектора, определенного в системе координат, которая может двигаться произвольным образом. В связи с этим введем понятия абсолютной и относительной производных вектора. Пусть даны основная система координат и подвижная система координат, которая совершает произвольное движение. Пусть какой-либо вектор определен в подвижной системе координат, т.е. проекции этого вектора на оси подвижной системы – заданные функции времени. Если i,j,k – единичные векторы подвижной системы координат, то вектор 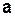может быть представлен в виде

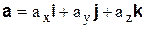. (7.1)

Дифференцируя обе части равенства (7.1) по времени, будем, иметь в виду, что векторы i,j и k вследствие движения подвижной системы координат меняют свое направление, т.е. являются функциями времени.

Таким образом, абсолютная производная вектора по времени будет равна

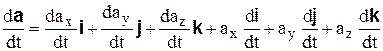. (7.2)

Сумма первых трех слагаемых, представляющая собой производную от вектора в подвижной системе координат, называется относительной или локальной производной

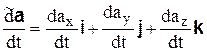. (7.3)

Заменяя в формулах (3.9) и (6.10) радиус-вектор 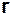последовательно на i,j и k, получим

.

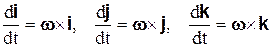Поэтому сумма последних трех слагаемых в (7.2) может быть представлена в виде

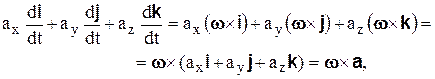(7.4)

где – угловая скорость подвижной системы координат.

Следовательно,

. (7.5)

Таким образом, абсолютная производная вектора равна сумме относительной производной этого вектора и векторного произведения угловой скорости подвижной системы координат на этот вектор.