Движение свободного твердого тела

 

Рассмотрим движение свободного твердого тела. Введем, кроме неподвижной системы координат Ох₁y₁z₁ еще подвижную систему координат Aх₂y₂z₂, перемещающуюся поступательно относительно осей Ох₁y₁z₁ и связанную с телом только в одной точке – точке А, и подвижную систему координат Axyz, жестко связанную с телом (рис. 6.6). В подвижной системе

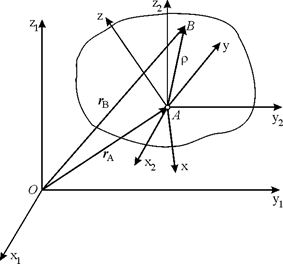Рис. 6.6.

координат Aх2y2z2 тело имеет одну закрепленную в ней точку – точку А, следовательно, тело в этой системе координат участвует в движении, рассмотренном нами в предыдущем параграфе. Для того чтобы задать положение тела в подвижной системе координат Aх2y2z2, можно ввести три угла Эйлера , а для определения

положения относительно неподвижной системы координат нужно, кроме того, задать положение точки А, для чего потребуется знать еще три величины: x_lA, y_lA, z_lA. Таким образом, положение свободного твердого тела определяется шестью независимыми параметрами: x_lA, y_lA, z_lA, .

Перейдем к определению скоростей точек свободного тела. Скорость произвольной точки В равна производной от ее радиуса-вектора по времени. Пользуясь рис. 6.6, найдем

.

Следовательно,

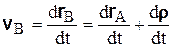. (6.19)

Заметим, что – скорость точки А; кроме того, вектор 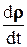представляет собой скорость точки В относительно подвижной системы координат Aх₂y₂z₂, в которой тело имеет одну закрепленную точку. Следовательно, согласно формуле (6.10) .

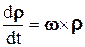Таким образом, формулу (6.19) можно переписать в виде

. (6.20)

Здесь – угловая скорость вращения тела относительно системы координат Aх₂y₂z₂. (Так же как и для плоского движения, можно показать, что угловая скорость не зависит от выбора полюса).

Формулу (6.20) можно прочитать следующим образом: скорость любой точки свободного твердого тела геометрически складывается из скорости произвольно выбранного полюса и скорости этой точки во вращательном движении тела относительно полюса.

Пользуясь формулой (6.20), можно доказать следующую теорему: