Ускорения точек тела, имеющего одну неподвижную точку
Задание движения. Углы Эйлера
Движение тела, имеющего одну неподвижную точку, называют сферическим движением или вращением тела вокруг неподвижной точки.
 Рис. 6.1.
Рис. 6.1.
| Твердое тело с одной закрепленной точкой имеет три степени свободы. Положение такого тела относительно неподвижной системы координат Ox1y1z1 (рис. 6.1), как правило, определяют при помощи углов Эйлера, которые вводятся следующим образом. |
Свяжем жестко с телом подвижную систему координат Охуz, выбрав начало координат в неподвижной точке О (рис. 6.1). Координатная плоскость хОу пересекается с неподвижной плоскостью x1Oy1 вдоль прямой ОК, которая называется линией узлов. Угол, составляемый неподвижной осью Ox1 с линией узлов, называется углом прецессии и обозначается буквой  . Угол, составляемый линией узлов с подвижной осью Ох, носит название угла собственного вращения и обозначается буквой
. Угол, составляемый линией узлов с подвижной осью Ох, носит название угла собственного вращения и обозначается буквой 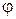 . Угол между осями Oz1 и Оz называется углом нутации и обозначается буквой
. Угол между осями Oz1 и Оz называется углом нутации и обозначается буквой  . Все углы отсчитываются соответственно от осей Ox1, ОК и Oz1 против хода часовой стрелки, как показано на рис. 6.1.
. Все углы отсчитываются соответственно от осей Ox1, ОК и Oz1 против хода часовой стрелки, как показано на рис. 6.1.
Покажем, что, зная три функции  ,
,  и
и  , можно всегда найти положение системы координат Охуz, а следовательно, и положение тела, скрепленного с ней. Действительно, откладывая от оси Ох1 угол прецессии
, можно всегда найти положение системы координат Охуz, а следовательно, и положение тела, скрепленного с ней. Действительно, откладывая от оси Ох1 угол прецессии  , мы найдем линию узлов ОК. Проведем через точку О плоскость, перпендикулярную линии узлов, и от оси Оz1 (эта ось должна лежать в построенной плоскости) отложим угол нутации
, мы найдем линию узлов ОК. Проведем через точку О плоскость, перпендикулярную линии узлов, и от оси Оz1 (эта ось должна лежать в построенной плоскости) отложим угол нутации  . Таким образом, будет определено положительное направление оси Оz. Через точку О проведем плоскость, перпендикулярную оси Оz; эта плоскость пройдет через линию узлов ОК. Отложим теперь в построенной плоскости от линии узлов угол собственного вращения
. Таким образом, будет определено положительное направление оси Оz. Через точку О проведем плоскость, перпендикулярную оси Оz; эта плоскость пройдет через линию узлов ОК. Отложим теперь в построенной плоскости от линии узлов угол собственного вращения 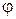 и определим положительное направление оси Ох. Ось Оу должна лежать в той же плоскости и составлять вместе с осями Ох и Оz правую систему координат. Таким образом, углы
и определим положительное направление оси Ох. Ось Оу должна лежать в той же плоскости и составлять вместе с осями Ох и Оz правую систему координат. Таким образом, углы  и
и 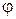 полностью определяют положение осей подвижной системы.
полностью определяют положение осей подвижной системы.
6.2. Распределение скоростей точек твердого тела,
имеющего одну неподвижную точку. Мгновенная ось вращения. Мгновенная угловая скорость
 Рис.6.2.
Рис.6.2.
| Пусть твердое тело имеет одну неподвижную точку О. Свяжем жестко с телом систему координат Охуz (рис. 6.2). Система координат Охуz однозначно определяет положение рассматриваемого тела по отношению к неподвижной системе отсчета Ох1y1z1. Положение произвольной точки твердого тела определяется |
радиусом-вектором  . Если х, у и z – координаты точки М в подвижной системе координат, a i,j и k – единичные векторы осей этой системы координат, то радиус-вектор можно представить в виде
. Если х, у и z – координаты точки М в подвижной системе координат, a i,j и k – единичные векторы осей этой системы координат, то радиус-вектор можно представить в виде
 . (6.1)
. (6.1)
В подвижной системе отсчета координаты х, у, z точки М являются постоянными величинами, т.е.  ,
,  ,
,  , а единичные векторы i, j, kбудут функциями времени, так как система координат Охуz движется вместе с твердым телом.
, а единичные векторы i, j, kбудут функциями времени, так как система координат Охуz движется вместе с твердым телом.
Дифференцируя (6.1) по 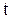 , получим скорость точки М
, получим скорость точки М
 . (6.2)
. (6.2)
Умножая обе части равенства (6.2) скалярно на i, j и k, получим
 (6.3)
(6.3)
Так как векторы i, j и k взаимно перпендикулярны, то
 (6.4)
(6.4)
Дифференцируя эти равенства по времени, найдем две группы формул:
 (6.5)
(6.5)
 (6.6)
(6.6)
Выражения (6.3) при этом примут вид
 (6.7)
(6.7)
Формулы (6.7) содержат три скалярные функции времени,
 ,
,
для которых введем обозначения:
 . (6.8)
. (6.8)
Перепишем теперь формулы (6.7) в виде
 (6.9)
(6.9)
Так как  ,
,
то, в соответствии с выражением (6.9), имеем
 .
.
Если теперь ввести вектор  с проекциями
с проекциями 
 ,
,
то скорость точки можно представить векторным произведением
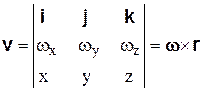 .
.
Итак, скорость точки тела, совершающего сферическое движение, определяется формулой
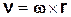 . (6.10)
. (6.10)
Геометрическое место точек, скорость которых равна нулю, определяется из уравнения
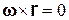 , (6.11)
, (6.11)
представляющего собой условие коллинеарности векторов  и
и 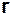 . Это векторное уравнение в системе координат Охуz можно записать в виде
. Это векторное уравнение в системе координат Охуz можно записать в виде
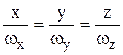 . (6.12)
. (6.12)
Уравнения (6.12) определяют прямою линию, направляющие косинусы которой пропорциональны проекциям  вектора
вектора  . В общем случае вектор
. В общем случае вектор  и его проекции
и его проекции  являются функциями времени, поэтому положение прямой (6.12) изменяется как относительно тела, так и относительно неподвижной системы координат Ох1y1z1.
являются функциями времени, поэтому положение прямой (6.12) изменяется как относительно тела, так и относительно неподвижной системы координат Ох1y1z1.
Прямая (6.12), в каждой точке которой скорости точек тела в данный момент равны нулю, называется мгновенной осью вращения. (Она также называется мгновенной осью скоростей.)
Введенный нами вектор  направлен по мгновенной оси вращения.
направлен по мгновенной оси вращения.
Как уже было установлено, скорость любой точки М тела определяется формулой (6.10), совпадающей по своей форме с выражением для скоростей точек твердого тела, вращающегося вокруг неподвижной оси с угловой скоростью  . Следовательно, скорости точек твердого тела, имеющего одну неподвижную точку, распределяются так, как если бы тело вращалось вокруг оси, совпадающей в данный момент с мгновенной осью вращения. В частности, модуль скорости точки М в данный момент определяется равенством
. Следовательно, скорости точек твердого тела, имеющего одну неподвижную точку, распределяются так, как если бы тело вращалось вокруг оси, совпадающей в данный момент с мгновенной осью вращения. В частности, модуль скорости точки М в данный момент определяется равенством 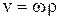 ,
,
где 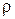 – расстояние от точки М до мгновенной оси вращения. Скорость точки М направлена перпендикулярно плоскости, проходящей через ее радиус-вектор
– расстояние от точки М до мгновенной оси вращения. Скорость точки М направлена перпендикулярно плоскости, проходящей через ее радиус-вектор  и мгновенную ось вращений (рис. 6.3).
и мгновенную ось вращений (рис. 6.3).
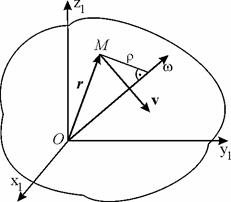 Рис. 6.3.
Рис. 6.3.
| По аналогии с вращением тела вокруг неподвижной оси назовем в рассматриваемом нами случае сферического движения тела вектор  вектором угловой скорости. При этом следует иметь в виду, что при вращении тела вокруг неподвижной оси вектор угловой скорости вектором угловой скорости. При этом следует иметь в виду, что при вращении тела вокруг неподвижной оси вектор угловой скорости  представляет собой вектор, представляет собой вектор,
|
всегда направленный по неподвижной оси вращения и характеризующий изменение во времени реального угла  поворота тела. Для тела, имеющего одну неподвижную точку, выражение «угловая скорость» имеет условный характер, т.к. положение тела определяется не одним, а тремя углами и, следовательно, нет такого одного угла, скорость изменения которого представил бы введенный вектор
поворота тела. Для тела, имеющего одну неподвижную точку, выражение «угловая скорость» имеет условный характер, т.к. положение тела определяется не одним, а тремя углами и, следовательно, нет такого одного угла, скорость изменения которого представил бы введенный вектор  . Кроме того, этот вектор может меняться и по модулю и по направлению. Проекции этого вектора на координатные оси являются функциями углов Эйлера и их первых производных.
. Кроме того, этот вектор может меняться и по модулю и по направлению. Проекции этого вектора на координатные оси являются функциями углов Эйлера и их первых производных.
Отметим, что из формул (6.8) для случая вращения твердого тела вокруг неподвижной оси, например, вокруг оси Oz, можно получить
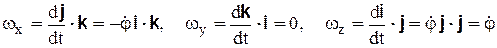 ,
,
т.к. 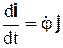 ,
,  ,
, 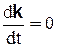 .
.
Если известны направления скоростей двух точек тела, то мгновенную ось вращения можно найти графически. Как следует из картины распределения скоростей точек тела в данный момент времени, мгновенная ось вращения лежит в плоскости, перпендикулярной направлению скорости точки тела, и проходит через неподвижную точку тела. Следовательно, если через точки тела, направления скоростей которых известны, провести плоскости, перпендикулярные этим скоростям, то линия пересечения этих плоскостей и будет мгновенной осью вращения.
Мгновенную ось вращения можно определить и в том случае, когда известна одна точка тела, скорость которой в данный момент времени равна нулю. Соединяя эту точку с неподвижной точкой тела, найдем мгновенную ось вращения.
Положение точки М тела в неподвижной системе координат определяется координатами х1, y1, и z1 а вектор  имеет проекции
имеет проекции 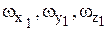 . Тогда, в соответствии с формулой (6.10), проекции скорости точки М на неподвижные оси координат будут
. Тогда, в соответствии с формулой (6.10), проекции скорости точки М на неподвижные оси координат будут
 (6.13)
(6.13)
Уравнение мгновенной оси вращения в неподвижной системе координат имеет вид
 . (6.14)
. (6.14)
Геометрическое место мгновенных осей вращений, построенных в неподвижной системе координат, называется неподвижным аксоидом, а в подвижной системе координат – подвижным аксоидом.
Из уравнений (6.14) следует
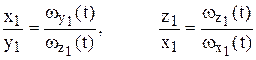 .
.
Полученные уравнения дают уравнение неподвижного аксоида в параметрическом виде; параметром служит время t. Исключая из этих уравнений t, можно получить уравнение конической поверхности (неподвижного аксоида) 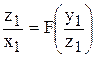 .
.
Аналогично, исключая время t из уравнений
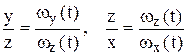 ,
,
полученных из формул (6.12), найдем уравнение подвижного аксоида
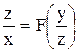 .
.
Введем прежде всего понятие углового ускорения. Угловым ускорением называется производная угловой скорости по времени, т.е.
 . (6.15)
. (6.15)
 Рис. 6.4.
Рис. 6.4.
| Из определения видно, что вектор углового ускорения можно рассматривать как скорость конца вектора  (рис. 6.4). Угловое ускорение (рис. 6.4). Угловое ускорение  направлено по касательной к годографу вектора угловой скорости (рис. 6.4), поэтому его направление может быть каким угодно в зависимости от закона изменения направлено по касательной к годографу вектора угловой скорости (рис. 6.4), поэтому его направление может быть каким угодно в зависимости от закона изменения
|
вектора угловой скорости. Заметим попутно, что годограф вектора угловой скорости – кривая, лежащая на неподвижном аксоиде (рис. 6.4).
Перейдем теперь к определению ускорения произвольной точки тела. Исходя из определения ускорения и используя равенство (6.10), получим
 .
.
Но 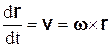 , а
, а  ,
,
следовательно,
 . (6.16)
. (6.16)
Таким образом, ускорение  может быть представлено как сумма двух ускорений:
может быть представлено как сумма двух ускорений:  и
и  .
.
Ускорение  называется вращательной составляющей ускорения. Модуль этого ускорения равен
называется вращательной составляющей ускорения. Модуль этого ускорения равен
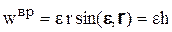 ,
,
где  – расстояние от точки М до вектора
– расстояние от точки М до вектора  . Направлено это ускорение перпендикулярно плоскости векторов
. Направлено это ускорение перпендикулярно плоскости векторов  и
и 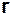 в ту сторону, откуда кратчайший переход от вектора
в ту сторону, откуда кратчайший переход от вектора  к вектору
к вектору 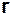 виден против хода часовой стрелки. Заметим, что вследствие несовпадения направлений угловой скорости и углового ускорения вращательная составляющая ускорения может быть направлена по отношению к направлению скорости под любым углом, оставаясь перпендикулярной вектору
виден против хода часовой стрелки. Заметим, что вследствие несовпадения направлений угловой скорости и углового ускорения вращательная составляющая ускорения может быть направлена по отношению к направлению скорости под любым углом, оставаясь перпендикулярной вектору 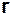 . В этом существенное различие между вращением твердого тела вокруг неподвижной оси и движением тела, имеющего одну неподвижную точку.
. В этом существенное различие между вращением твердого тела вокруг неподвижной оси и движением тела, имеющего одну неподвижную точку.
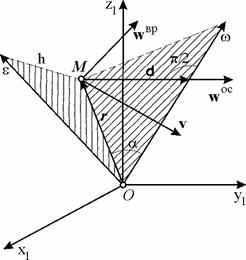 Рис. 6.5.
Рис. 6.5.
| Ускорение  направлено по перпендикуляру к плоскости векторов направлено по перпендикуляру к плоскости векторов  и и  , т.е. по направлению вектора d (рис. 6.5), имеющего начало в точке М и конец в основании перпендикуляра, опущенного из точки М на мгновенную ось вращения. Модуль векторного произведения , т.е. по направлению вектора d (рис. 6.5), имеющего начало в точке М и конец в основании перпендикуляра, опущенного из точки М на мгновенную ось вращения. Модуль векторного произведения  равен равен 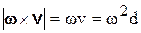 ,
т.к. ,
т.к. 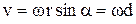 . .
|
Следовательно, можно записать
 . (6.17)
. (6.17)
Это ускорение называется осестремительной составляющей ускорения.
Итак, ускорение любой точки тела равно сумме вращательной и осестремительной составляющих ускорения
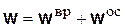 . (6.18)
. (6.18)