Полярные координаты
Пусть координаты точки заданы как функции времени 
Согласно (3.14) имеем  .
.
На основании (3.18) получим
 ,
,
но так как  ,
,  ,
,
то  .
.
Отсюда находим проекции ускорения на радиальное и поперечное направления
 (9.22)
(9.22)
Модуль и направление вектора ускорения определяются по формулам
 ,
,

3.3.2. Ускорение при естественном способе задания движения
Предварительно познакомимся с необходимыми сведениями из дифференциальной геометрии. Рассмотрим пространственную кривую. Пусть  – единичный вектор касательной, проведенной в какой-либо – единичный вектор касательной, проведенной в какой-либо
|  Рис. 3.13.
Рис. 3.13.
|
точке М этой кривой (рис. 3.13). Возьмем теперь на кривой точку М1, близкую к точке М, и обозначим единичный вектор касательной в этой точке через  . Параллельно перенеся вектор
. Параллельно перенеся вектор  в точку М, проведем плоскость через векторы
в точку М, проведем плоскость через векторы  и
и  приложенные в точке М.
приложенные в точке М.
При стремлении точки М1 к точке М эта плоскость в пределе займет определенное положение. Полученную таким образом плоскость называют соприкасающейся плоскостью в точке М. Отметим, что если рассматриваемая кривая плоская, то она целиком будет расположена в соприкасающейся плоскости.
Плоскость, проведенную через точку М перпендикулярно касательной, называют нормальной плоскостью. Линия пересечения соприкасающейся и
| нормальной плоскостей определяет главную нормаль к кривой в точке М. Плоскость, проведенную через точку М перпендикулярно главной нормали, называют спрямляющей плоскостью. На рис. 3.14 соприкасающаяся, |  Рис. 3.14.
Рис. 3.14.
|
нормальная и спрямляющая плоскости обозначены соответственно цифрами I, II и III.
Линия пересечения спрямляющей и нормальной плоскостей определяет бинормаль к кривой.
Таким образом, в каждой точке кривой можно указать три взаимно перпендикулярных направления: касательной, главной нормали и бинормали. Принимая эти направления за координатные оси, введем единичные векторы этих осей.
Единичный вектор касательной  нами уже был введен. Единичный вектор
нами уже был введен. Единичный вектор  , направленный в сторону вогнутости кривой, будет единичным вектором главной нормали. Направление единичного вектора бинормали
, направленный в сторону вогнутости кривой, будет единичным вектором главной нормали. Направление единичного вектора бинормали  определим из требования, чтобы касательная, главная нормаль и бинормаль, направления которых определяются векторами
определим из требования, чтобы касательная, главная нормаль и бинормаль, направления которых определяются векторами  ,
,  ,
,  , образовывали правую систему осей, т.е.
, образовывали правую систему осей, т.е.  Полученный трехгранник, составленный из соприкасающейся, нормальной и спрямляющей плоскостей, называется естественным трехгранником. Векторы
Полученный трехгранник, составленный из соприкасающейся, нормальной и спрямляющей плоскостей, называется естественным трехгранником. Векторы  ,
,  ,
,  являются единичными векторами осей естественного трехгранника (рис. 3.14).
являются единичными векторами осей естественного трехгранника (рис. 3.14).
Обозначим через  величину угла между вектором
величину угла между вектором  , проведенным в точке М, и вектором
, проведенным в точке М, и вектором  , проведенным в точке М1, близкой к точке М. Этот угол называется углом смежности (рис. 3.15 а).
, проведенным в точке М1, близкой к точке М. Этот угол называется углом смежности (рис. 3.15 а).
 Рис. 3.15.
Рис. 3.15.
|
Кривизной кривой в точке М называют предел отношения угла смежности  к абсолютному значению длины дуги
к абсолютному значению длины дуги  , т.е.
, т.е.
 . (3.23)
. (3.23)
Радиусом кривизны кривой в точке М называется величина, обратная кривизне
 . (3.24)
. (3.24)
Вектор скорости согласно выражению (3.17) можно представить в виде
 .
.
На основании формулы (3.18) имеем
 . (9.25)
. (9.25)
Определим величину и направление вектора  .
.
Пусть в момент времени 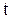 точка находится в положении М на траектории, а в момент времени
точка находится в положении М на траектории, а в момент времени  – в положении М1. Перенося вектор их в точку М, найдем приращение вектора
– в положении М1. Перенося вектор их в точку М, найдем приращение вектора  за промежуток времени
за промежуток времени  (рис. 3.15 а)
(рис. 3.15 а)
 .
.
Вектор  при движении точки в сторону положительного отсчета дуги направлен в сторону вогнутости траектории (рис. 3.15 а), а при движении точки в сторону отрицательного отсчета дуги направлен в сторону выпуклости траектории (рис. 3.15 б). Найдем производную вектора
при движении точки в сторону положительного отсчета дуги направлен в сторону вогнутости траектории (рис. 3.15 а), а при движении точки в сторону отрицательного отсчета дуги направлен в сторону выпуклости траектории (рис. 3.15 б). Найдем производную вектора  :
:
 .
.
Вектор  всегда направлен в сторону вогнутости траектории (см. рис. 3.15 а и б) и лежит в плоскости, проходящей через точку М и векторы
всегда направлен в сторону вогнутости траектории (см. рис. 3.15 а и б) и лежит в плоскости, проходящей через точку М и векторы  и
и  (плоскость МАВ). Следовательно, вектор
(плоскость МАВ). Следовательно, вектор  лежит в соприкасающейся плоскости, т.к. при
лежит в соприкасающейся плоскости, т.к. при  плоскость МАВ совпадает с соприкасающейся плоскостью к траектории в точке М.
плоскость МАВ совпадает с соприкасающейся плоскостью к траектории в точке М.
Дифференцируя тождество  по
по  , получим
, получим
 ,
,
т.е. скалярное произведение  на
на  равно нулю, а это значит, что вектор
равно нулю, а это значит, что вектор  перпендикулярен
перпендикулярен  . Таким образом, вектор
. Таким образом, вектор  лежит в соприкасающейся плоскости, направлен в сторону вогнутости траектории и перпендикулярен
лежит в соприкасающейся плоскости, направлен в сторону вогнутости траектории и перпендикулярен  ; следовательно, он направлен по главной нормали к центру кривизны.
; следовательно, он направлен по главной нормали к центру кривизны.
Определим теперь модуль вектора  . Из равнобедренного треугольника АМВ (см. рис. 3.15 а) найдем
. Из равнобедренного треугольника АМВ (см. рис. 3.15 а) найдем 
или, используя равенства (3.23) и (3.24), получим
 .
.
Учитывая, что  есть единичный вектор главной нормали, будем иметь
есть единичный вектор главной нормали, будем иметь
 .
.
Значит,  ,
,
и, следовательно,
 , (3.26)
, (3.26)
т.к.  .
.
Из этой формулы следует, что вектор ускорения лежит в соприкасающейся плоскости.
Составляющие ускорения по направлениям  и
и  соответственно равны
соответственно равны
 .
.
Проекция ускорения на направление 
 (3.27)
(3.27)
называется касательным (тангенциальным) ускорением. Проекция ускорения на главную нормаль
 (3.28)
(3.28)
называется нормальным ускорением. Касательное ускорение характеризует изменение модуля скорости, а нормальное ускорение характеризует изменение скорости по направлению. Модуль вектора ускорения равен
 . (3.29)
. (3.29)
Касательное ускорение  равно нулю при движении точки с постоянной по модулю скоростью и в моменты времени, в которые скорость
равно нулю при движении точки с постоянной по модулю скоростью и в моменты времени, в которые скорость  достигает экстремальных значений.
достигает экстремальных значений.
Если  и
и  одного знака, то модуль скорости
одного знака, то модуль скорости  точки возрастает и движение в этом случае называется ускоренным. Если же
точки возрастает и движение в этом случае называется ускоренным. Если же  и
и  разных знаков, то модуль скорости
разных знаков, то модуль скорости  точки убывает и движение будет замедленным. При
точки убывает и движение будет замедленным. При  модуль скорости остается постоянным – движение равномерное.
модуль скорости остается постоянным – движение равномерное.