Декартова система координат

Пусть движение точки задано в декартовой системе координат, принятой за неподвижную, т.е. пусть заданы координаты точки как функции времени

, , .

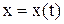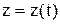Согласно выражению (3.6) имеем .

Так как единичные векторы выбранной системы координат постоянны, то на основании формулы (3.9) получаем

.

Рис. 3.8.

На рис. 3.8 показано разложение скорости на составляющие по осям координатной системы Oxyz. Таким образом, проекции скорости , , на координатные оси будут , , .

т.е. проекция скорости точки на координатную ось равна первой производной по времени от соответствующей этой оси координаты.