Вектора по скалярному аргументу всегда направлена по касательной к годографу этого вектора.
2.4. Основные правила дифференцирования вектор-функций.
1. Если  – постоянный вектор, то
– постоянный вектор, то  .
.
2. Производная суммы вектор-функций равна сумме производных слагаемых
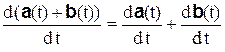 .
.
3. Пусть вектор-функция  умножается на скалярную функцию
умножается на скалярную функцию 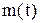 того же скалярного аргумента. Тогда
того же скалярного аргумента. Тогда
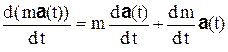 .
.
4. Производные скалярного и векторного произведения вектор-функций соответственно определяются выражениями:
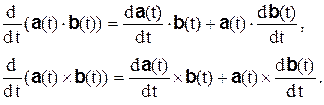
Пусть вектор-функция 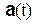 задана в неподвижной прямоугольной системе координат; тогда
задана в неподвижной прямоугольной системе координат; тогда
 ,
,
где 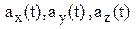 – проекции вектор-функции
– проекции вектор-функции  на оси
на оси 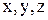 (рис. 2.2). Так как векторы
(рис. 2.2). Так как векторы  постоянные, то
постоянные, то
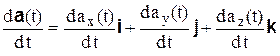 .
.
С другой стороны, вектор  можно записать через его проекции следующим образом:
можно записать через его проекции следующим образом:
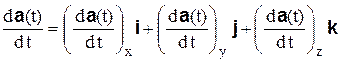 .
.
Сравнивая оба выражения, найдем проекции производной вектора на координатные оси
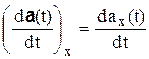 ,
, 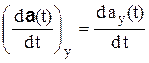 ,
, 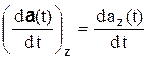 .
.
Следовательно, проекции производной вектора на неподвижные оси равны производным от соответствующих проекций вектора.
Модуль производной определяется из равенства
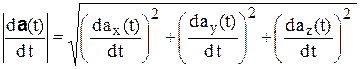 .
.
Если модуль вектор-функции  остается постоянным при изменении аргумента
остается постоянным при изменении аргумента 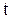 , то годографом вектор-функции
, то годографом вектор-функции  будет кривая, расположенная на сфере радиуса а. Следовательно, производная
будет кривая, расположенная на сфере радиуса а. Следовательно, производная  , направленная по касательной к годографу вектор-функции
, направленная по касательной к годографу вектор-функции  , будет в этом случае перпендикулярна вектору
, будет в этом случае перпендикулярна вектору  .
.
2.5. Интегрирование вектор-функции скалярного аргумента.
Вектор-функция 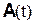 называется первообразной функцией для вектор-функции
называется первообразной функцией для вектор-функции  при
при 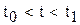 , если
, если 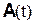 дифференцируема и
дифференцируема и
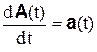 ,
, 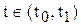 .
.
Неопределенным интегралом от вектор-функции скалярного аргумента  называется совокупность всех первообразных для
называется совокупность всех первообразных для 
 ,
,
где 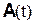 – какая-нибудь из первообразных для
– какая-нибудь из первообразных для  ;
;
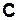 – произвольный постоянный вектор.
– произвольный постоянный вектор.
Для интегралов от вектор-функций справедливы следующие свойства
1. 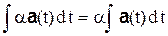 ,
, 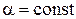 .
.
2. 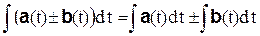 .
.