Построение закона движения ведомого звена
A 4 D
BK
Рисунок 3 – Построение заданного и крайних положений механизма
При закрепленном звене 4 механизм - кривошипно-коромысловый. Звено 1 совершает полный оборот - кривошип, звено 2 движется плоско – параллельно - шатун, звено 3 совершает возвратно – вращательное движение – коромысло.
В кривошипно–коромысловом механизме, как и в кривошипно–ползунном, выходное звено (коромысло или ползун) может занимать два крайних положения. В нашем случае коромысло 3 может занимать крайнее правое или крайнее левое положения. При этом расстояние между точкой А и точкой С механизма будет наибольшим или наименьшим. Чем левее точка С, тем она ближе к Аи тем меньше угол ÐCBA. Точка Смаксимально приблизится к А, когда ÐCBA = 0, т.е. точки А,В и Срасположатся на одной линии. Тогда:
ACmin = BC – AB.
Точка С максимально удалится от точки А, когда ÐCBA = 180°, т.е. точки А,В,С расположатся снова на одной линии. Тогда:
AC0 = AB + BC.
Точка Смеханизма движется по траектории, представляющей собой дугу окружности радиуса DC. Сделав засечку на траектории точки С радиусом AC0 = AB + BC находим крайнее правое положение точки C0, сделав засечку радиусом ACK = BC – AB находим крайнее левое положение точки CK. Соединив соответственно точки A, BK, CK и Dнаходим крайнее левое положение механизма, а соединив точки A, B0, C0 и D– крайнее правое положение механизма.
Угол между двумя крайними положениями коромысла называется максимальным углом качания коромысла- βmax.
При кинематическом исследовании механизма целесообразно одно из крайних положений считать нулевым или начальным.
Если кривошип АВ вращается равномерно, то время для перехода коромысла с крайнего правого положения в крайнее левое будет больше, чем при переходе его с крайнего левого в крайнее правое положение, т.к. углы поворота кривошипа различны. Это обстоятельство используется при проектировании механизмов, имеющих рабочий и холостой ход. Рабочий ход выполняется по заданной технологии при меньшей скорости рабочего звена, холостой ход - при большей скорости. Например, в строгальных, долбежных станках холостой ход выполняется с большей скоростью, чем рабочий.
Для построения траектории любой точки механизма строится ряд следующих друг за другом положений механизма и полученные положения заданной точки соединяют плавной кривой. По траектории точки механизма можно определить также ее перемещение. Для этого необходимо измерить длину отрезка траектории на интересующем нас участке перемещения точки и умножить на μl. При этом получим истинное значение перемещения точки механизма.
Чтобы получить закон движения ведомого звена, т.е. изменение положения ведомого звена в функции времени β3 = f1(t) или в функции движения ведущего звена β3 = f2(φ) при заданном законе движения входного звена, изображают ряд положений ведущего звена равноотстоящих друг от друга. Обычно число положений ведущего звена принимают не менее 12. За начальное положение принимают одно из крайних положений механизма. В нашем случае (рис. 3) начальным является крайнее правое положение механизма. Начиная с точки B0окружность радиуса АВделится на 12 равных частей по ходу вращения кривошипа (ω1). Строится ряд последовательных положений механизма. Для каждого положения ведущего и ведомого звеньев измеряются углы φi и βi от начального положения. С учетом выбранных масштабных коэффициентов μφ и μβ по оси абсцисс откладываем отрезки, соответствующие значениям φi (xi = φi · μφ) , а по оси ординат откладываем отрезки, соответствующие значениям βi (yi = βi · μβ). Полученные точки соединяем плавной кривой (рис.4) и получаем графическое изображение закона движения ведомого звена в функции угла поворота ведущего звена. Если угловая скорость ведущего звена постоянна ω1 = const, то в этом случае легко перейти к β3 = f1(t).
β
βmax
0 1 2 3 Рисунок 4 – График движения ведомого звена |
Для кривошипно-ползунного механизма аналогичным образом строится зависимость S = f2(φ) или S = f1(t) - закон перемещения ползуна в зависимости от положения кривошипа, или при ω1 = const - в функции времени.
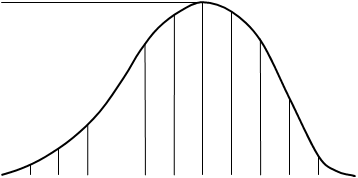


 4 5 6 7 8 9 10 11 12 φ(t)
4 5 6 7 8 9 10 11 12 φ(t)