Кинематические характеристики звена и точки
Точке свойственны линейныекинематические характеристики. Траектория точки - линия - след точки. Кинематическими характеристиками точки являются:
перемещение S[м], S = f(t) ;
|
линейная скорость V[м/с], V = ;
|
линейное ускорение a [м/с²], a = = .
Иногда можно встретить выражение «точка вращается». Для того, чтобы выяснить, объект враща-
ется или нет, нужно в нем зафиксировать линию и проследить, есть ли вращение объекта вокруг оси, перпендикулярной плоскости или нет. Точка – бесконечно малый объект по размерам стремящийся к нулю. В точке линию провести нельзя. Поэтому при исследовании кинематических характеристик точек механизма говорить о угловых кинематических характеристиках точки не приходится.
Звену свойственны угловые кинематические характеристики. В общем случае звено обладает только угловыми кинематическими характеристиками, исключая поступательное движение:
угол поворота или угловое перемещение j [рад], j = f(t);
|
угловая скорость w [рад/с], w = ;
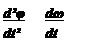 |
угловое ускорение e [рад/с²], e = = .
В общем случае движения звена понятие линейной скорости звена лишено смысла, т.к. скорости различных точек звена различны. Можно говорить о средней линейной скорости звена, если имеем в виду некоторую среднюю скоростей всех точек звена. Однако к этому термину нужно относиться осторожно, применять его только там, где в этом есть необходимость.
Исключение составляет поступательно движущееся звено, у которого скорости всех точек одинаковы. Только в этом случае звено имеет линейные кинематические характеристики.