КИНЕМАТИКА ТОЧКИ

ВВЕДЕНИЕ

 

В кинематике изучается движение материальных объектов (точки, твердого тела, сплошной среды) без рассмотрения причин его вызывающих или изменяющих это движение.

Пространство в классической механике считается эвклидовым, не зависящим от времени и движущихся в нем материальных объектов. Время принимается универсальным, не связанным с пространством и не зависящим как от движения наблюдателя, с точки зрения которого рассматривается движение материального объекта, так и от движения самого материального объекта.

Движение материального объекта всегда следует рассматривать относительно какого-либо твердого тела – тела отсчета, т.е. движение является относительным. С телом отсчета скрепляют систему осей координат, например декартовых, принимая ее за систему отсчета.

В курсе теоретической механики обычно изучаются движение точки и твердого тела.

В кинематике точки рассматриваются характеристики движения точки, такие, как скорость, ускорение, и методы их определения при различных способах задания движения. Траекторией точки называется геометрическое место ее последовательных положений в пространстве с течением времени относительно рассматриваемой системы отсчета.

1. ВЕКТОРНЫЙ СПОСОБ ИЗУЧЕНИЯ ДВИЖЕНИЯ

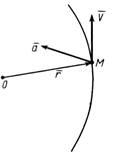
При векторном способе движение задается радиусом-вектором 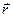этой точки (рис. 1). Движение точки считается заданным, если известен радиус-вектор движущейся точки как функция времени, т. е.

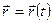
Задание векторного уравнения движения полностью определяет движение точки. Траекторией точки является годограф радиуса-вектора.

Годографом вектора называют геометрическое место его концов, если переменный вектор в различные моменты времени откладывать от одной и той же общей точки.

2. СКОРОСТЬ ТОЧКИ

Одной из основных характеристик движения точки является ее скорость относительно выбранной системы отсчета (рис. 2). Положение точки М определяется в момент времени t радиусом-вектором. В другой момент времени 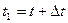точка займет положение M₁. За время радиус-вектор движущейся точки изменится на .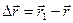

При этом средняя скорость точки определится выражением:

Скорость точки в данный момент времени определится, как предел средней скорости, если промежуток времени, за который определяется средняя скорость, стремится к нулю, т. е.

.

Таким образом, скорость точки равна первой производной по времени от ее радиуса-вектора. Она направлена по касательной к траектории в сторону движения точки.

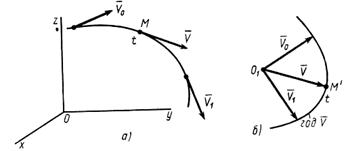
Годографом вектора скорости является линия, на которой располагаются концы этого вектора в различные моменты времени, если их начала совместить в одной общей точке. Для построения годографа вектора скорости выбираем точку, например O₁ (рис. 3, б), и начала векторов скорости для различных моментов времени переносим в эту точку, не изменяя их величин и направлений. Каждой точке траектории М (рис. 3, а) будет соответствовать своя изображающая точка М' на годографе вектора скорости (рис. 3, б).

При равномерном движении точки по прямой годографом вектора скорости является одна точка; при неравномерном движении - отрезок прямой, параллельный траектории.