Барометрические формулы

На основании уравнений статики устанавливаются закономерности распределения давления, плотности и массы воздуха по высоте. В своем дифференциальном виде () они позволяют выполнить расчет лишь для малых приращений высоты.

Для определения давления в слоях конечной толщины уравнения статики необходимо записать в интегральном виде, которые носят название барометрических формул.

Проинтегрируем () от уровня моря, где давление р0, до произвольной высоты z, где давление р. Имеем 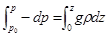, откуда .

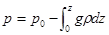Другую интегральную форму уравнению статики можно придать, если воспользоваться уравнением состояния влажного воздуха (). Подставив найденное отсюда значение r, перепишем () в виде. Интегрируя от 0 до z и от р0 до р, получаем: .

Однородная атмосфера. Предположим, что плотность воздуха в пределах всей атмосферы не изменяется с высотой, т.е. r=r0=const.

Здесь r0 – плотность воздуха при z=0. Такая атмосфера носит название однородной. Пренебрежем зависимостью ускорения свободного падения от высоты. Тогда на основании () получаем барометрическую формулу однородной атмосферы:

. ()

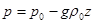Согласно этой формуле давление убывает с высотой по линейному закону. В приложении к атмосфере формулу ()дает заведомо далекое от реальных условий распределение давления. Однако для гидросферы, плотность которой изменяется в очень узких пределах, формула ()дает вполне удовлетворительные результаты.

Высота однородной атмосферы . Поскольку , то 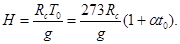Отсюда следует, что высоты однородной атмосферы конечна и зависит только от температуры воздуха на поверхности Земли. При Т=0°С она составляет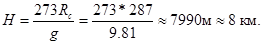

В соответствии с уравнением состояния 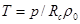. Вертикальный градиент температуры

Таким образом. температура в однородной атмосфере убывает по линейному закону , при этом градиент значительно больше среднего в атмосфере.

2.4. Изменение плотности воздуха с высотой.

Рассмотрим вопрос в общем случае. С этой целью прологафмируем, а затем продифференцируем уравнение состояния :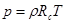

.

Заменив dp/dz в соответствии с (1) и подставив в полученное выражение r из уравнения состояния, найдем:

, или . ()

Формула справедлива для любого распределения температуры воздуха по высоте. Возможны три различных случая изменения плотности с высотой.

1. Если g>gA=3.42 °С/100 м, то , т.е. плотность воздуха возрастает с высотой. Вертикальные градиенты температуры превышающие 3.42 °С/100 м в реальных условиях могут наблюдаться лишь в дневные часы (летом) в приземном слое атмосферы. При таких условиях плотность в этом слое увеличивается с высотой.

2. Если g=gA, то , т.е. плотность воздуха не изменяется с высотой. Это случай однородной атмосферы.

3. Если g<gA=3.42 °С/100 м, то 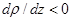, т.е. плотность воздуха убывает с высотой. Этой случай является преобладающим. Выше приземного слоя g<gA при любых состояниях атмосферы. В приземном случае g<gA наблюдается также значительно чаще, чем случаи g>gA.