Уравнения статики атмосферы

Силы, действующие в атмосфере в состоянии равновесия

СТАТИКА АТМОСФЕРЫ

Система находится в равновесии (покое), если результирующая всех сил, действующих на систему равна нулю.

Силы подразделяются на массовые и поверхностные.

Массовыми силами, действующими на атмосферу в целом и на ее части, являются сила тяжести и отклоняющая сила вращения Земли (кориолисова сила).

Поверхностные силы, действующие в атмосфере, - это сила давления и сила трения.

Однако кориолисова сила и сила трения появляются лишь при движении атмосферы относительно поверхности Земли или одних ее частей относительно других. Поэтому силами, действующими в атмосфере в состоянии покоя, являются сила тяжести и сила давления.

Пусть атмосфера находится в состоянии покоя по отношению к земной поверхности. Тогда горизонтальная составляющая градиента давления должна обращаться в нуль (в противном случае воздух придет в движение). Для этого необходимо и достаточно, чтобы изобарические поверхности совпадали с уровенными.

Выделим в атмосфере две изобарические поверхности, расположенные на высотах z и z+dz (рис.). Между изобарическими поверхностямиp p+dp выделим объем воздуха с горизонтальными основаниями 1 м². На нижнее основание действует сила давления p, направленное снизу вверх; на верхнее – сила давления p+dp, направленная сверху вниз. Силы давления, действующие на боковые грани выделенного объема взаимно уравновешиваются.

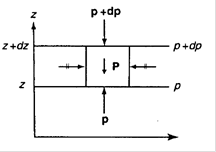
Рис. К выводу уравнения статики.

 

На этот объем действует сила тяжести Р, направленная по вертикали вниз и равная по модулю

.

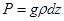Спроектируем все силы на ось z. Поскольку сумма всех сил равна нулю, то и сумма этих проекций равна нулю:

.

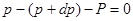Подставив выражение силы тяжести, получим .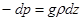

Разделив на dz определим второй вид основного уравнения статики атмосферы:

.

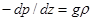Левая часть представляет собой вертикальную составляющую градиента давления, правая – силу тяжести, действующую на единичный объем воздуха. Таким образом, уравнение статики выражает равновесие двух сил – градиента давления и силы тяжести.

Из уравнения статики можно сделать три важных вывода:

1. Увеличению высоты (dz>0) соответствует отрицательное приращение давления (dp>0), что означает убывае давления с высотой. Уравнение статики выполняется с высокой точностью и в случае движения атмосферы.

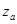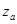2. Выделим в атмосфере вертикальный столб воздуха с основанием 1м2 и высотой от уровня z до верхней границы атмосферы . Вес этого столба равен . Проинтегрировав обе части () в пределах от z , где давление р, до , давление равно 0 (по определению верхней границы), получим: 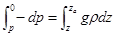, или .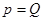

Таким образом, приходим ко второму определения понятия давления. Атмосферное давление на каждом уровне равно весу столба воздуха единичного поперечного сечения и высотой от данного уровня до верхней границы атмосферы. Отсюда понятен физический смысл убывания давления с высотой.

3. Уравнения статики позволяют сделать вывод о скорости убывания давления с высотой. Уменьшение давления тем больше, чем больше плотность воздуха и ускорение свободного падения. Основную роль играет плотность. Плотность воздуха с увеличением высоты падает. Чем выше расположен уровень, тем меньше убывание давления.

Если точки расположены на одной и той же изобарической поверхности, то плотность воздуха будет зависеть только от температуры в этих точках. В точке с более низкой температурой плотность выше. Это означает, что при подъеме на одну и ту же высоту понижение давления в точке с более высокой температурой меньше, чем в точке с более низкой температурой.

В холодной воздушной массе давление с высотой убывает быстрее, чем в теплой. Подтверждением этого вывода является тот факт, что на высотах (в средней и верхней тропосфере) в холодных воздушных массах преобладает низкое давление, а в теплых – высокое.

Оценим значение вертикального градиента. При нормальных условиях вблизи уровня моря r=1.29 кг/м3, g=9.81 м/с2. Подставив эти значения в (), найдем: G=12ю5 гПа/100м.