Электромагнитные волны
Лекция № 17
Электродинамика
Общая характеристика теории Максвелла
На прошлых лекциях нами были рассмотрены основные законы электрических и электромагнитных явлений: теорема Остроградского-Гаусса, закон полного тока и закон электромагнитной индукции. Эти законы, являясь обобщением экспериментальных фактов, позволяют по заданному распределению зарядов и токов отыскать созданные ими электрические и магнитные поля.
В 60-х годах прошлого столетия Максвелл, основываясь на идеях Фарадея, разработал законченную теорию электромагнитного поля.
Мы коротко остановимся на существе идей Максвелла и содержании его теории.
1. Теория Максвелла является феноменологической. Электрические и магнитные свойства среды описываются в ней с помощью трех величин: относительной диэлектрической проницаемости  , относительной магнитной проницаемости
, относительной магнитной проницаемости 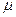 и удельной электропроводности
и удельной электропроводности 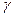 . Зависимость этих величин от свойств среды, внутренний механизм явлений, происходящих в среде при поляризации и намагничивании в теории не рассматривается.
. Зависимость этих величин от свойств среды, внутренний механизм явлений, происходящих в среде при поляризации и намагничивании в теории не рассматривается.
2. Теория Максвелла является макроскопической теорией. В ней рассматриваются электрические и магнитные поля, создаваемые зарядами, которые сосредоточены в объемах, неизмеримо больших объемов атомов и молекул. Расстояние от источников полей до рассматриваемых точек в них также много больше размеров молекул, а периоды измерения переменных электрических и магнитных полей много больше периодов внутримолекулярных процессов.
3. В теории Максвелла рассматриваются усредненные электрические и магнитные поля, непрерывно изменяющиеся в каждой точке пространства, причем это усреднение производится для интервалов времени значительно больших периодов колебания элементарных зарядов с объемами, превышающими объемы атомов и молекул.
4. Теория Максвелла является теорией близкодействия. Согласно этой теории скорость распространения электрических и магнитных взаимодействий равна скорости света в данной среде.
Первое уравнение Максвелла
Обобщение Максвеллом закона электромагнитной индукции состояло в следующем. Как мы знаем, ЭДС индукции в неподвижном замкнутом контуре выражается формулой
 .
.
Так как
 ,
,
то
 .
.
При этом в правой части уравнения применен символ частной производной по времени. Это сделано потому, что у нас имеется производная по времени от вектора 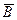 в фиксированной точке поверхности (т.е. берем производную только по времени).
в фиксированной точке поверхности (т.е. берем производную только по времени).
Тогда
 . (1)
. (1)
С другой стороны, при изучении понятия электродвижущей силы мы получили формулу для любой ЭДС, которая справедлива и для ЭДС индукции:
 ,
,
где 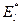 - напряженность поля сторонних сил.
- напряженность поля сторонних сил.
Общая напряженность поля, обусловленная возникновением в контуре ЭДС индукции, складывается из напряженности поля сторонних сил  и напряженности электростатического поля
и напряженности электростатического поля  , т.е.
, т.е.
 .
.
Откуда
 .
.
Следовательно,
 ,
,
где 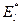 ,
,  ,
,  - проекции векторов на направление
- проекции векторов на направление  .
.
Подставив это выражение в последнюю формулу для ЭДС индукции, получим:
 .
.
В силу потенциальности электростатического поля:
 .
.
Тогда
 .
.
Приравняв это выражение для ЭДС индукции к формуле (1), получим:
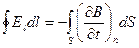 .
.
Это выражение является одним из основных в электромагнитной теории Максвелла.
Циркуляция вектора напряженности электрического поля по произвольному замкнутому контуру  равна взятой с обратным знаком скорости изменения магнитного потока сквозь поверхность, ограниченную контуром. Т.е. переменное магнитное поле создает в замкнутом проводящем контуре вихревое электрическое поле.
равна взятой с обратным знаком скорости изменения магнитного потока сквозь поверхность, ограниченную контуром. Т.е. переменное магнитное поле создает в замкнутом проводящем контуре вихревое электрическое поле.
Максвелл обобщил этот закон, доказав, что электрическое поле возбуждается не только в веществах, где имеются заряды, но и в вакууме. Иными словами переменное магнитное поле в любой точке пространства создает вихревое электрическое поле, независимо от того находится ли в этой точке проводник или нет. Обобщенное таким образом последнее выражение называется первым уравнением Максвелла в интегральной форме.
Бетатрон
Явление возникновения в пространстве вихревого электрического поля под влиянием переменного магнитного поля было использовано для создания индукционного ускорителя электронов – бетатрона.
Основными элементами бетатрона являются электромагнит с коническими полюсными наконечниками и вакуумная ускорительная камера, имеющая форму замкнутого кольца.
 Обмотка электромагнита питается переменным током, частота которого составляет сотни герц.
Обмотка электромагнита питается переменным током, частота которого составляет сотни герц.
Изменение силы тока в обмотке электромагнита вызывает изменение магнитного поля в пространстве между полюсами электромагнита и возникновение вихревого электрического поля.
В момент времени, когда 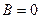 , в камеру подают пучок электронов, получаемых с помощью термоэлектронной эмиссии в специальном источнике, расположенном внутри камеры.
, в камеру подают пучок электронов, получаемых с помощью термоэлектронной эмиссии в специальном источнике, расположенном внутри камеры.
Когда магнитное поле начинает возрастать, образующееся при этом электрическое поле подхватывает электроны и разгоняет их. Траекториями электронов являются окружности, совпадающие с линиями напряженности вихревого электрического поля.
За время нарастания магнитного поля (~ ) электроны успевают сделать до миллиона оборотов и приобретают энергию в несколько сотен МЭВ. При такой энергии масса электрона в сотни раз превышает массу покоя, а скорость его приближается к скорости света.
) электроны успевают сделать до миллиона оборотов и приобретают энергию в несколько сотен МЭВ. При такой энергии масса электрона в сотни раз превышает массу покоя, а скорость его приближается к скорости света.
Для того чтобы электрон двигался по орбите постоянного радиуса 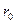 , между магнитной индукцией поля на орбите и внутри нее должно выполняться определенное соотношение. Найдем его.
, между магнитной индукцией поля на орбите и внутри нее должно выполняться определенное соотношение. Найдем его.
Циркуляция вектора напряженности по круговой орбите радиуса 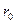 равна:
равна:
 .
.
С другой стороны, согласно первому уравнению Максвелла
 .
.
Приравняв оба эти выражения, получим
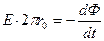 .
.
Откуда
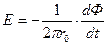 .
.
Нас будет в дальнейшем интересовать лишь величина напряженности поля, поэтому знак (-) мы в дальнейшем опустим.
Уравнения движения электронов запишутся следующим образом:
а) действие магнитного поля
 ,
,
где  - центростремительное ускорение.
- центростремительное ускорение.
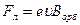 - сила Лоренца,
- сила Лоренца,
 - магнитная индукция поля на орбите.
- магнитная индукция поля на орбите.
Тогда
 или
или 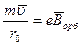 . (2)
. (2)
б) действие электрического поля
 - закон сохранения момента импульса,
- закон сохранения момента импульса,
где  - сила, действующая на электрон со стороны электрического поля.
- сила, действующая на электрон со стороны электрического поля.
 .
.
Тогда
 .
.
Проинтегрировав это выражение по 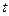 , получим
, получим
 .
.
Так как магнитное поле перпендикулярно плоскости орбиты электрона, то
 ,
,
где 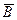 - среднее по площади орбиты значение магнитной индукции.
- среднее по площади орбиты значение магнитной индукции.
Тогда
 .
.
Сравнивая это уравнение с выражением (2) мы видим, что
 .
.
Таким образом, для того, чтобы электрон все время двигался по орбите радиуса 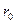 , магнитная индукция на орбите должна составлять половину среднего значения магнитной индукции внутри орбиты. Это достигается за счет изготовления полюсных наконечников в виде усеченных конусов.
, магнитная индукция на орбите должна составлять половину среднего значения магнитной индукции внутри орбиты. Это достигается за счет изготовления полюсных наконечников в виде усеченных конусов.
Для устойчивости электрона на орбите необходимо, чтобы при случайных радиальных отклонениях электрона возникали силы, возвращающие его снова на орбиту. Для этого необходимо, как показывают расчеты, чтобы пространственное распределение магнитного поля обеспечивало его убывание от центра к периферии медленнее, чем  , где
, где  - расстояние от данной точки поля до его оси симметрии.
- расстояние от данной точки поля до его оси симметрии.
Применяются бетатроны главным образом в ядерных исследованиях. Небольшие ускорители на энергию до  нашли применение в промышленности, как источники очень жесткого рентгеновского излучения, используемого для целей дефектоскопии массивных изделий.
нашли применение в промышленности, как источники очень жесткого рентгеновского излучения, используемого для целей дефектоскопии массивных изделий.
Токи смещения. Опыт Эйхенвальда
Ранее мы видим, что всякое переменное магнитное поле вызывает вихревое электрическое поле. Анализируя различные электромагнитные процессы, Максвелл пришел к выводу, что существует и обратное явление: всякое изменение электрического поля вызывает появление вихревого магнитного поля.
Для установления количественных характеристик между изменяющимся электрическим и возникающим магнитным полем Максвелл ввел понятие тока смещения.
Рассмотрим цепь квазистационарного переменного тока, содержащую конденсатор.
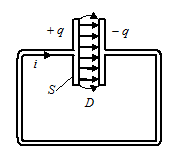 Движение свободных носителей заряда, т.е. ток проводимости, имеет место во всей цепи, кроме зазора между обкладками конденсатора. В пространстве между обкладками конденсатора имеется переменное электрическое поле, которое можно характеризовать вектором электрического смещения
Движение свободных носителей заряда, т.е. ток проводимости, имеет место во всей цепи, кроме зазора между обкладками конденсатора. В пространстве между обкладками конденсатора имеется переменное электрическое поле, которое можно характеризовать вектором электрического смещения 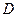 . Это переменное электрическое поле Максвелл назвал током смещения.
. Это переменное электрическое поле Максвелл назвал током смещения.
Согласно гипотезе Максвелла токи проводимости в металлическом проводнике замыкаются токами смещения в диэлектрике.
Обозначим через  площадь пластин и через
площадь пластин и через 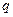 - заряд на обкладках конденсатора.
- заряд на обкладках конденсатора.
Из электростатики нам известно, что поверхностная плотность заряда на обкладках конденсатора 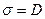 .
.
Т.к.  , то и
, то и  . Откуда
. Откуда  .
.
Сила тока проводимости
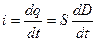 .
.
Разделив обе части этого равенства на  с учетом того, что
с учетом того, что  , получим
, получим  - плотность тока проводимости.
- плотность тока проводимости.
Правая часть этого уравнения показывает скорость изменения электрического поля в диэлектрике. Равенство этих двух векторов ( и
и  ) на границе проводник-диэлектрик показывает, что величина
) на границе проводник-диэлектрик показывает, что величина  как бы продолжает линии тока через диэлектрик и замыкает их. По предложению Максвелла эту величину принято называть плотностью тока смещения:
как бы продолжает линии тока через диэлектрик и замыкает их. По предложению Максвелла эту величину принято называть плотностью тока смещения:
 .
.
В диэлектрике вектор смещения, как известно, состоит из двух слагаемых
 ,
,
где  - напряженность поля в диэлектрике;
- напряженность поля в диэлектрике;
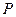 - вектор поляризации.
- вектор поляризации.
С учетом этого
 ,
,
где первое слагаемое представляет собой плотность тока смещения в вакууме, а второе – плотность поляризационного тока.
Ток смещения в вакууме не выделяет джоулевой теплоты. Ток поляризации выделяет теплоту, связанную с трением в процессе поляризации диэлектрика.
 Эту формулу, определяющую плотность тока смещения, Максвелл распространил и на электрические поля любого вида, в том числе и на вихревые. Из всех физических свойств, присущих току проводимости, Максвелл приписал току смещения лишь одно – способность создавать в окружающем пространстве магнитное поле. Следует обратить внимание, что ток смещения определяется производной вектора
Эту формулу, определяющую плотность тока смещения, Максвелл распространил и на электрические поля любого вида, в том числе и на вихревые. Из всех физических свойств, присущих току проводимости, Максвелл приписал току смещения лишь одно – способность создавать в окружающем пространстве магнитное поле. Следует обратить внимание, что ток смещения определяется производной вектора 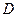 , а не самим этим вектором. Так, например, в случае плоского конденсатора вектор
, а не самим этим вектором. Так, например, в случае плоского конденсатора вектор 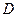 направлен от положительной пластины к отрицательной.
направлен от положительной пластины к отрицательной.
Если электрическое поле увеличивается, то  и, следовательно, ток смещения направлены от «+» к «-» (см. рис.).
и, следовательно, ток смещения направлены от «+» к «-» (см. рис.).
 Если электрическое поле убывает, то
Если электрическое поле убывает, то  направлено от отрицательной пластины к положительной и магнитное поле направлено противоположно предыдущему случаю.
направлено от отрицательной пластины к положительной и магнитное поле направлено противоположно предыдущему случаю.
Из всего вышеизложенного следует один важный вывод: конденсатор в цепи переменного тока не разрывает цепь. Переменный ток проходит через конденсатор в виде тока смещения, т.е. изменения электрического поля конденсатора.
Согласно теории Максвелла при расчетах магнитных полей в формулы, где входит плотность тока, нужно подставлять сумму плотности тока проводимости и плотности тока смещения, т.е.
 ,
,
где  .
.
В общем случае электрическое поле может быть неоднородным и может зависеть не только от времени, но и от координат. Тогда выражение для плотности тока смещения будет иметь вид  , где знак этой частной производной указывает на то, что магнитное поле зависит только от быстроты изменения электрического смещения во времени.
, где знак этой частной производной указывает на то, что магнитное поле зависит только от быстроты изменения электрического смещения во времени.
Тогда
 .
.
В общем случае токи проводимости и токи смещения не разделены в пространстве, как это имеет место в конденсаторе. Все типы токов существуют в одном и том же объеме и можно говорить о полном токе, равном сумме тока проводимости и тока смещения, т.е.
 .
.
Максвелл обобщил закон полного тока, введя в его правую часть полный ток, охватываемый замкнутым контуром с площадью  .
.
В общем виде, как нам известно, закон полного тока записывается, как
 или
или  .
.
С учетом поправки Максвелла
 (т.к.
(т.к.  ).
).
В общем случае, если площадка  не перпендикулярна к вектору
не перпендикулярна к вектору  , то в этом выражении вместо
, то в этом выражении вместо  нужно взять составляющую плотности тока
нужно взять составляющую плотности тока  , перпендикулярную к
, перпендикулярную к  . Тогда
. Тогда
 - второе основное уравнение Максвелла.
- второе основное уравнение Максвелла.
Экспериментальное определение токов смещения было впервые произведено Эйхенвальдом в 1901 г. Он изучал магнитное поле тока поляризации, который, как мы знаем, является частью тока смещения.
Опыт Эйхенвальда состоял в следующем: