Решение.

Предварительные вычисления представим в таблице, приняв , .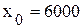

Группы предприятий по объему выпуска, тонн	Число предприятий в % к итогу
1000 - 3000			-4000	-2			-24
3000 - 5000			-2000	-1			-20
5000 - 7000
7000 - 9000
9000 - 11000
							-6

Тогда .

Использование метода моментов для определения дисперсии позволяет значительно упростить громоздкие вычисления. При этом если частоты имеют достаточно большой общий делитель, то целесообразно их сократить на эту величину. В этом случае значение дисперсия не изменится.

Среднее квадратическое отклонение определяется как квадрат-ный корень из дисперсии:

- для совокупности:

;

- для ряда распределения:

.

Коэффициент вариации можно определить как отношение среднего квадратического отклонения и средней величины признака:

.

Чем больше значение коэффициента вариации, тем менее однородной является совокупность и тем менее точно среднее значение признака характеризует изучаемое явление. Наоборот, чем меньше значение коэффициента вариации, тем более однородной является совокупность и тем более точно среднее значение признака характеризует изучаемое явление:

- если − совокупность считается неоднородной;

- если − совокупность можно считать однородной;

- если − совокупность считается однородной.

Рассмотренные показатели вариации используются для статистической оценки уровня экономического риска. Уровень экономического риска, рассчитанный через размах вариации, среднее линейное отклонение и среднее квадратическое отношение, имеет стоимостное выражение, через коэффициент вариации, измеряется в процентах, а через дисперсию является безразмерной величиной. В любом случае, чем меньше величина рассматриваемого показателя вариации, тем ниже уровень экономического риска изучаемого экономического явления или процесса. Для оценки экономического риска рекомендуется сравнивать его уровень с размером риска за предыдущие периоды или со среднеотраслевым значением.

Принято считать, что если уровень экономического риска, рассчитанный через коэффициент вариации, не превышает 25-30 %, то существует достаточно высокая вероятность получения средней (ожидаемой, запланированной) величины изучаемого признака и, наоборот.

6.2. Дисперсия может быть определена с помощьюправила сложения дисперсий:

,

где - общая дисперсия;

- средняя из внутригрупповых (групповых, частных) дисперсий;

- межгрупповая дисперсия.

Для использования правила сложения дисперсий соответствующим образом должна быть представлена статистическая информация. Ряд распределения должен включать группировки по двум признакам. Один из группировочных признаков является результативным, а другой − факторным. Результативный признак является результатом воздействия одной или нескольких причин и выступает в качестве основной характеристики объекта исследования. Факторный признак определяет поведение результативного и выступает в качестве причины изменения его величины. Например, объем производства продукции является результативным признаком по отношению к среднегодовой стоимости основных средств, среднему остатку оборотных средств и среднесписочной численности работников предприятия, которые выступают в качестве факторных признаков.

Общая дисперсия характеризует изменение (вариацию) изучаемого (результативного) признака под действием на него всех без исключения факторов (факторных признаков).

Внутригрупповая дисперсия характеризует изменение (вариацию) изучаемого (результативного) признака в пределах группы под действием на него всех факторов, кроме фактора, положенного в основание группировки:

,

где - количество выделенных групп по факторному признаку;

- i-тое значение результативного признака j-той группы;

- среднее значение результативного признака j-той группы;

- частота i-го значения результативного признака j-той группы.

Таким образом, количество внутригрупповых дисперсий определяется числом групп, выделенных по факторному признаку.

Средняя из внутригрупповых дисперсий рассчитывается:

,

где - частота (количество элементов) j-той группы.

Межгрупповая дисперсия характеризует изменение (вариацию) изучаемого (результативного) признака под действием на него фактора (факторного признака), положенного в основание группировки:

,

где - среднее значение признака для всего ряда распределения.

Для определения тесноты связи между результативным (изучаемым) и факторным (положенным в основание группировки) признаками используются следующие два статистических показателя:

- коэффициент детерминации:

.

Коэффициент детерминации изменяется в интервале от 0 до 1. Чем ближе значение показателя к единице, тем теснее связь между признаками, чем ближе к нулю, тем связь слабее. Если показатель равен единицы, связь между признаками считается функциональной, а если равен нулю, связь − отсутствует.

- корреляционное отношение:

.

Данный показатель, в отличие от коэффициента детерминации, помимо тесноты связи определяет ее направление. Корреляционное отношение изменяется в интервале от -1 до 1. Если показатель имеет положительное значение связь считается прямой, а отрицательное − обратной.

Пример 6.2. Распределение рабочих трех предприятий одного объединения по тарифным разрядам характеризуется следующими данными:

Тарифный разряд рабочего	Численность рабочих на предприятии
предприятие 1	предприятие 2	предприятие 3

Определить: 1) дисперсию по каждому предприятию (внутригрупповые дисперсии); 2) среднюю из внутригрупповых дисперсий; 3) межгрупповую дисперсию; 4) общую дисперсию.