Средняя арифметическая
Средняя арифметическая – наиболее распространенный вид средней. Она используется тогда, когда объем варьирующего признака определяется как сумма его значений у отдельных единиц совокупности.
В зависимости от характера исходных данных используется простая или взвешенная средняя арифметическая.
Например, заработная плата рабочих участка составляет 310, 360, 370, 390 и 410 грн. Средняя заработная плата рабочих участка определяется по формуле простой средней арифметической:
 (грн.)
(грн.)
Но в практике аналитической работы часто возникает потребность расчета средних на основе сгруппированных данных. В этом случае используется средняя арифметическая взвешенная:
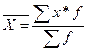 (4.1)
(4.1)
Несколько условный характер носит расчет средней интервального ряда распределения. В этом случае в качестве варианты используется среднее значение интервала, определяемое как полусумма значений нижней и верхней границ. Ширину открытого интервала условно принимают равной соседнему (или исходя из содержания признака). Расчет средней по данным интервального ряда является приближенным, т.к. предполагается, что отдельные варианты равномерно распределены внутри интервала.
Средняя арифметическая обладает следующими свойствами:
1. Алгебраическая сумма отклонений вариантов от средней равна нулю.
2. Если каждый вариант уменьшить или увеличить на какую – нибудь величину, то средняя изменится соответственно на ту же величину.
3. Если каждый вариант осредняемого признака разделить или умножить на любое число, то средняя увеличится или уменьшится в такое же число раз.
4. Если частоту каждого значения признака увеличить или уменьшить в n раз, величина средней не изменится.
Изложенные свойства позволяют упростить ее расчеты путем преобразований вариантов осредняемого признака.
Формула средней арифметической взвешенной, рассчитанная по способу моментов:
 (4.2)
(4.2)
где  – начало отсчета или условный нуль;
– начало отсчета или условный нуль;
h - величина интервала;
 - средняя новых вариантов.
- средняя новых вариантов.
 (4.3)
(4.3)
Величины  и h могут быть произвольными, однако наиболее простые расчеты, когда h – величина интервала, а
и h могут быть произвольными, однако наиболее простые расчеты, когда h – величина интервала, а  - одна из центральных вариант ряда, если ряд имеет нечетное число признаков, при четном – одна из вариант с максимальной частотой.
- одна из центральных вариант ряда, если ряд имеет нечетное число признаков, при четном – одна из вариант с максимальной частотой.