Перестановка членов ряда

Признак Коши

Теорема 18. Если числовой ряд 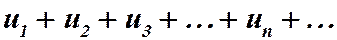(27) таков, что существует предел то при ряд (27) сходится и при том абсолютно, при ряд (27) расходится. При признак Коши не дает ответа на вопрос о сходимости или расходимости ряда.

 

Теорема 19. Если члены абсолютно сходящегося ряда переставить каким-либо образом, то получим ряд, который абсолютно сходится, и его сумма равна сумме исходного ряда.

Эта теорема выражает переместительное свойство абсолютно сходящихся рядов. Для условно сходящихся рядов переместительное свойство не справедливо. Более того, имеет место следующая теорема.

Теорема 20. (теорема Римана). Если ряд сходится не абсолютно, то переставляя его члены, можно добиться того, что вновь полученный ряд будет иметь любую наперед заданную сумму.

В частности, переставляя члены ряда, можно добиться расходимости вновь полученного ряда.