Достаточные признаки сходимости рядов с положительными членами

Перестановка членов ряда

Теорема 9. Если члены сходящегося ряда с положительными членами переставить каким-либо образом, то вновь полученный ряд будет сходящимся, и его сумма будет равна сумме исходного ряда.

1) Признак сравнения.

Теорема 10. Пусть даны два ряда с положительными членами : (15)

(16)

и при любом п выполняется неравенство:

Тогда, если ряд (16) сходится, то и ряд (15) сходится. Если ряд (15) расходится, то и ряд (16) расходится.

Доказательство. Пусть для рядов (15) и (16) условия теоремы выполняются. Обозначим через п-ю частичную сумму ряда (15), а через п-ю частичную сумму ряда (16).

Так как по условию то, очевидно, (17)

Пусть ряд (16) сходится. Обозначим сумму ряда через

Так как ряд (16) есть ряд с положительными членами, то при любом п. при любом п.

Таким образом, последовательность частичных сумм 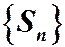ряда (15) строго возрастает и ограничена сверху числом. По теореме Вейерштрасса последовательность 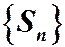имеет конечный предел, то есть ряд (15) сходится. Пусть ряд (15) расходится, тогда Переходя к пределу в (17), будем иметь: Предел в левой части неравенства равен а значит, и справа Следовательно, ряд (16) расходится. Теорема доказана.

Пример 10. Исследовать на сходимость ряд:

Решение. Рассмотрим ряд: .

Это ряд геометрической прогрессии и следовательно, ряд сходится.

При любом псправедливо: Значит, ряд тоже сходится.

Замечание 3. Теорема сохраняет силу и в том случае, когда неравенство выполняется не при любом п, а лишь начиная с некоторого номера.

2) Признак Даламбера.

Теорема 11. Если ряд с положительными членами (15) таков, что существует предел то при ряд (15) сходится, а при ряд (15) расходится.

Замечание 4. Если , то признак Даламбера не дает ответа на вопрос о сходимости ряда. В этом случае нужно исследовать ряд на сходимость другими методами.

Пример 20.11. Исследовать ряд на сходимость:

Решение.

Ряд сходится.