Остаток ряда

Пусть дан числовой ряд 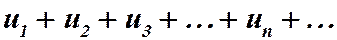(8)

Отбросив первые п членов данного ряда, получим ряд: (9). Ряд (9) называется п-ым остатком ряда.

Теоремы о связи между сходимостью или расходимостью ряда и его остатка:

Теорема 3. Если числовой ряд (8) сходится или расходится, то соответственно сходится или расходится любой его остаток.

Обратная теорема 4. Если сходится или расходится какой-нибудь остаток ряда, то соответственно сходится или расходится этот ряд.

Следствие1. Прибавление к ряду или отбрасывание от него конечного числа членов не влияет на его сходимость.

Следствие 2. Если S – сумма ряда (8), частичная сумма этого ряда, а сумма п-го остатка, то справедливо:

Теорема 5. Если числовой ряд сходится, то предел суммы его п-го остатка равен 0 при

Доказательство. Пусть ряд (8) сходится, тогда справедливо где сумма ряда, п-ая частичная сумма этого ряда, остаток ряда: (10)

Так как то переход к пределу при в (10) дает нам 0. Теорема доказана.