Пример операции сложения.
А = 0,3 ; В = 15,8.
Формат ЕС ЭВМ (число разрядов мантиссы m=12).
А = (0,3)10 = (0,4(С))16 · 160
МА
1 округление к ближайшему
0 1 7 8 19
В = (15,8)10 = (F,(C))16 = (0,F(C))16 · 16
MB
0 1 7 8 19
1) XA = _1 0 0 0 0 0 0
XB = 1 0 0 0 0 0 1
(XA-XB)доп.= 1 1 1 1 1 1 1
(XA-XB)доп. = 0000001 (-1) ХС=ХВ
А>0, B>0. 
 |
| |
3) МА = . 0 0 0 0 0 1 0 0 1 1 0 0
МВ = . 1 1 1 1 1 1 0 0 1 1 0 1
1 . 0 0 0 0 0 0 0 1 1 0 0 1
Результат сложения денормализован влево.
| |
 |
4) МС = . 0 0 0 1 0 0 0 0 0 0 0 1
Т.к. выполнен сдвиг мантиссы влево, то характеристику результата нужно увеличить на 1 (ХС+1).
С
0 1 7 8 19
С* = МС · 16Рс = (0,101)16 · 162 = (10,1)16 = 16,0625
Несмотря не то, что оба операнда за счет округления были представлены с избытком , результат получился представленным с недостатком. Этот факт можно объяснить потерей значащих младших разрядов сначала у первого операнда при выравнивании порядков, а затем и у результата при его нормализации.
В принципе, погрешность полученного результата можно объяснить следующими факторами:
• неточным представлением операндов;
• потерей значащих разрядов мантиссы одного из операндов при
уравнивании порядков;
• потерей значащих разрядов мантиссы результата при его нормализации сдвигом мантиссы вправо.
АС = СТ - С* = 0,0375 ,
где АС –абсолютная погрешность;
СТ –точное значение;
С* - приближенное значение.
δА =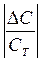 
· 100% ,
где δА – относительная погрешность.
Умножение чисел с плавающей запятой
Операция умножения сводится к сложению порядков как целых чисел и перемножению мантисс сомножителей как дробных чисел с фиксированной запятой.
В связи с тем, что, независимо от знака, мантиссы чисел с плавающей запятой представляются в прямом коде, то для умножения мантисс целесообразно использовать метод умножения в прямых кодах. Т.к. порядки сомножителей представлены не в явном виде, а со смещением (в виде характеристик), то для получения характеристики результата (произведения) необходимо выполнить следующие операции над характеристиками операндов:
+ХА = РА + d C = A·B
ХB = РB + d
ХА+ХB = РА+РB+2d
PC
XC=PC+d
XC = XA + XB – d
При использовании правильных дробей для представления мантисс сомножителей результат перемножения мантисс может находиться в следующих пределах:
Замечание: будем считать, что в операции умножения участвуют именно нормализованные числа с плавающей запятой.
1/S ≤ MA < 1
1/S ≤ MB < 1
1/S2 ≤ MC=MA·MB < 1
Из полученного соотношения следует, что результат умножения двух нормализованных мантисс может оказаться денормализованным вправо, но максимум – на одну цифру (разряд).
Действительно:
S = 2 → MCmin = 0,01 ;
S = 16 → MCmin = (0,01)16 = (0,00000001)2.
Умножение чисел с плавающей точкой в стандарте IEEE-754 имеет ряд дополнительных нюансов.
Методы ускорения операции умножения
В связи с тем, что операция умножения является достаточно массовой, по крайней мере при решении научно-технических задач (по статистике доля операций умножения в программах научно-технического профиля составляет порядка 5%), значительное внимание разработчиков ЭВМ уделяется различным способам ускорения операции умножения. Эти способы ускорения принято разделять на два класса (вида):
- аппаратные (схемные);
- логические (алгоритмические).
Схемные методы сводятся к построению быстродействующих схем суммирования, а так же схем, называемых матричными умножителями. Матричный умножитель 8×8 позволяет выполнить умножение байтных сомножителей за один такт.
Логические методы ускорения основаны на одновременном анализе нескольких разрядов множителя и выполнений соответствующих действии над СЧП, в зависимости от анализируемых комбинаций. В практике построения схем АЛУ в основном используются методы ускоренного умножения на 2 и 4 разряда множителя.
Ускоренное умножение на 2 разряда множителя (в СМ ЭВМ)
Для определенности будем считать, что реализация метода осуществляется с использованием способа умножения от младших разрядов множителя со сдвигом СЧП вправо. Идея метода состоит в анализе пары младших разрядов множителя на каждом шаге умножения. После выполнения действий над СЧП, соответствующих анализируемой паре, производится сдвиг СЧП и множителя на 2 разряда вправо.
Возможны следующие комбинации пары разрядов:
00 –производится только сдвиг вправо на 2 разряда, СЧП сохраняется;
01 – производится сложение СЧП с множимым и последующий сдвиг на 2 разряда вправо;
10 – СЧП складывается с удвоенным множимым (сложение с удвоенным множимым соответствует сложению со сдвинутым на 1 разряд влево множимым), множимое подается на вход сумматора не прямо, а с перекосом влево;
11 – производится вычитание множимого из СЧП с последующим сдвигом на 2 разряда вправо. При этом используют так называемую корректирующую единицу, которую необходимо учитывать при умножении на следующую пару разрядов множителя путем сложения единицы с этой парой.
11 = 100-01 (в данной паре умножение производится на –(01), которое реализуется сложением СЧП с (-А)).
Другим способом реализации является вычитание множимого из старших разрядов СЧП.
В связи с необходимостью учета возможной добавки к очередной паре разрядов множителя в схему умножителя обычно вводится дополнительный бит для фиксации так называемого признака коррекции, поэтому выполняемое на каждом шаге действие над СЧП определяется не только парой младших разрядов множителя, но и значением этого признака. С учетом признака коррекции выполняемые действия можно свести к следующей таблице:
| Пара младших разрядов множителя | Признак коррекции для этой пары | Действия, выполняемые над СЧП | Признак коррекции для следующей пары |
| - +А +2А -А | |||
| +А +2А -А - |
Особенности реализации метода
• В связи с тем, что выполняемые над СЧП действия включают в себя как сложение, так и вычитание множимого, СЧП необходимо рассматривать как знаковое число (применительно к перемножению мантисс операндов с плавающей запятой).
• Поскольку одной из добавок к СЧП является 2А, для представления которого понадобится один дополнительный старший разряд, необходимо представления результата сложения расширить СЧП на 2 старших разряда (для сохранения переноса, который может иметь место при сложении с удвоенным множимым). С учетом же знакового представления СЧП для явного отображения знака понадобится еще один дополнительный старший разряд.
• В связи со знаковым представлением СЧП, его сдвиг вправо для корректного представления выполняется как арифметический. Это означает, что в освобождающиеся при сдвиге старшие разряды производится копирование знакового разряда СЧП.
• Если после завершения умножения сохраняется единичное значение признака коррекции, необходимо выполнить дополнительный шаг, на котором к СЧП прибавляется множимое (как для пары (01)), после чего сдвиг не выполняется.