Следы прямых
Рис. 28
Рис. 27.
Прямые (линии уровня ― (AB, CD, EF) пересекающиеся под прямым углом с прямыми общего положения (BN, DM, GK).
Как видно из рис.27, горизонтальная проекция прямого угла L ABN,а именно L A’ B’ N’,представляет собой прямой угол
(L90°), фронтальная проекция прямого угла L CDM,а именно
LC”D”M”,представляет собой прямой угол (90°), профильная
L проекция прямого угла L KGF,а именно L K”’G”’F”’,представляет собой прямой угол (90°), что соответствует выводам теоремыо частном случае проецирования прямого угла.
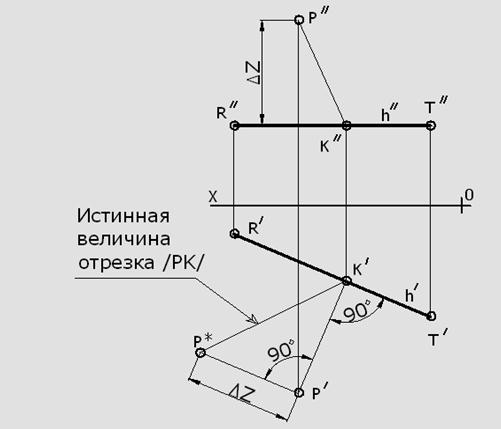В качестве примера применения теоремы о частном случае проецирования прямого угла рассмотрим задачу определения расстояния от точки «P» до прямой «h»(рис.28).
Заданы:Прямая «h»(горизонтальная) и точка «P»
Определить: Расстояние от точки «P» до прямой «h».
Алгоритм решения задачи:
1.Из точки «P»проводится перпендикуляр к прямой «h».
Выполняем подробное описание необходимых построений.
2.Определяется истинная величина отрезка перпендикуляра между точкой «P»и точкой пересечения перпендикуляра и прямой «K».
Прямая линия «h» –горизонтальная прямая, т.е. прямая параллельна горизонтальной плоскости проекций π1. Следовательно, горизонтальная проекция перпендикуляра (P’K’), проведенного из точки «P» к прямой «h» образует с горизонтальной проекцией прямой h’ угол равный 90 градусов.
Здесь точка «K»есть точкапересечения перпендикуляра (PK)с прямой «h».
Далее, пользуясь методом прямоугольного треугольника (см. стр. 19 данного пособия), определяем истинную величину отрезка │PK│.
Строится прямоугольный треугольник по двум катетам.
Первым катетом является горизонтальная проекция перпендикуляра – (P’K’).
Вторым катетом будет отрезок (ΔZ) равный разности расстояний концов отрезка │PK│до горизонтальной плоскости проекций π1, т.е. той плоскости, на которой мы взяли проекцию (P’K’) в качестве первого катета.
Длина гипотенузы построенного треугольника (Δ P’K’P*) (см. рис.29) является истинной величиной расстояния от точки «P»до прямой «h».
Примечание: Следы прямых необходимы для построения следов плоскостей.
Точки в которых заданная прямая пересекает плоскости проекций называют следами прямой.
При наличии на чертеже трех плоскостей проекций (π1 , π2 иπ3) мы можем иметь три следа заданной прямой:
Точку пересечения заданной прямой с горизонтальной плоскостью проекций называют горизонтальным следом прямой.
Точку пересечения заданной прямой с фронтальной плоскостью проекций называют фронтальным следом прямой.
Точку пересечения заданной прямой с профильной плоскостью проекций называют профильным следом прямой.
2.5.5.1 Обозначение следов прямых на чертежах
Горизонтальные следы: M (M’ M’’ M’’’), M1 (M1’ M1’’ M1’’’)……
Фронтальные следы: N (N’ N’’ N’’’), N1 (N1’ N1’’ N1’’’)……
Профильные следы: P (P’ P’’ P’’’), P1 (P1’ P1’’ P1’’’)……
2.5.5.2 Построение следов прямых на чертежах
2.5.5.2.1 Модель построения следов прямой общего положения (рис.29)
