Плоскости общего и частного положения

Способы задания плоскости. Комплексный чертеж плоскости

Рисунок 9

 

б) Прямые частного положения – это прямые, занимающие по отношению к плоскостям проекций особое положение, т.е. либо параллельные, либо перпендикулярные плоскостям проекций.

Первый подкласс прямых частного положения – прямые уровня. Это прямые, параллельные какой-либо плоскости проекций.

Горизонталь – прямая параллельная горизонтальной плоскости П1. Комплексный чертёж такой прямой изображён на рисунке 10.

 

	α

Рисунок 10

 

Фронтальная проекция горизонтали всегда параллельна прямой Х, а угол между осью Х и горизонтальной проекцией горизонтали составляет угол между прямой и фронтальной плоскостью проекций. Символическая запись: h // П1; a = Ðh П2.

β

Фронталь – прямая параллельная фронтальной плоскости П2. Комплексный чертёж фронтали изображён на рисунке 11.

 

Рисунок 11

 

Горизонтальная проекция фронтали параллельна оси Х, а угол b - угол наклона фронтали к горизонтальной плоскости проекций; f 2 // П2,

b = Ðf1П1.

Профильная прямая – это прямая, параллельная профильной плоскости П3. Комплексный чертёж профильной прямой изображён на рисунке 12. Горизонтальная и фронтальная проекции профильной прямой перпендикулярны оси Х, а углы a и b - соответственно, углы наклона прямой к плоскостям П1 и П2.

 

 

 

Рисунок 12.

 

Рисунок 12

 

Истинная величина прямых уровня или, так называемая натуральная величина, отображена на тех плоскостях, которым параллельны эти прямые.

Второй подкласс прямых частного положения – проецирующие прямые. Это прямые, перпендикулярные какой-либо плоскости проекций. К таким прямым относятся: горизонтально–проецирующая, фронтально-проецирующая и профильно-проецирующая прямые.

Их комплексные чертежи изображены соответственно на рисунке 13 (а, б, в).

 

 

 

а б в

 

Рисунок 13

 

Натуральная величина горизонтально-проецирующей прямой – её фронтальная проекция, фронтально-проецирующей прямой – её горизонтальная проекция, а профильно-проецирующей прямой – её горизонтальная и фронтальная проекции.

 

 

а) три точки, не лежащие на одной прямой;

 

Рисунок 14

 

б) прямая и точка, не лежащая на ней;

 

 

Рисунок 15

 

в) две параллельные прямые;

 

Рисунок 16

 

 

г) две пересекающиеся прямые;

 

Рисунок 17

 

д) плоская фигура (многоугольник, круг и т.д.).

 

 

 

Плоскость общего положения не параллельна и не перпендикулярна ни одной из плоскостей проекций.

 

 

Рисунок 18

 

Плоскости частного положения аналогично прямой подразделяются на плоскости уровня и проецирующие плоскости. На рисунке 19 (а,б,в) изображены, соответственно, горизонтальная, фронтальная и профильная плоскости. Причём горизонтальная плоскость задана двумя параллельными прямыми, фронтальная и профильная плоскости – двумя пересекающимися прямыми.

а б в

 

Рисунок 19

 

На рисунке 20 (а,б,в) показаны проецирующие плоскости. Горизонтально-проецирующая (рис. 20а) задана треугольником, фронтально-проецирующая (рис. 20б) - параллельными прямыми и профильно-проецирующая (рис. 20в) – пересекающимися прямыми.

 

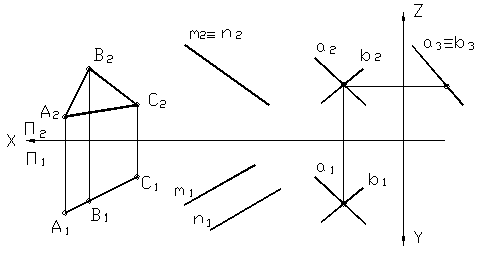А б в