Лекция №2

Контрольные вопросы

Рисунок 4

Рисунок 3

 

Для того, чтобы по проекциям точки А получить её истинное положение в пространстве, необходимо иметь две её проекции на плоскость П. Точка пересечения лучей, восстановленных из точки А1 и А2 параллельно S1 и S2, будет являться точкой А.

Частным случаем параллельного проецирования является ортогональное проецирование. При этом направление проецирования всегда перпендикулярно плоскости проекций (рисунок 4).

 

 

 

В случае ортогонального проецирования, для того чтобы определить положение точки в пространстве по её проекции, необходимо ввести дополнительную плоскость проекций П2, которая была бы перпендикулярна П1 (рисунок 5).

 

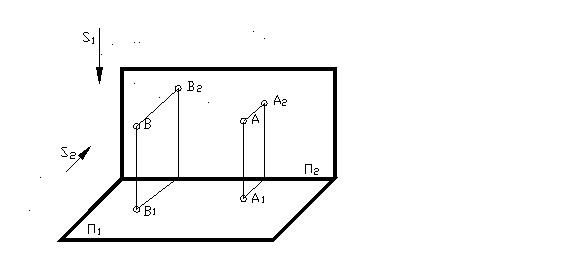Рисунок 5

 

На рисунке 5 показано построение проекций точки А на две взаимно ортогональные плоскости П1 и П2. И наоборот, имея две проекции точки А – А1 и А2, мы всегда можем получить положение точки А в пространстве, восстановив перпендикуляры к плоскостям проекций.

Преимущества ортогонального проецирования:

1. Простота графических построений для определения ортогональных проекций.

2. Возможность сохранить при определённых условиях на проекциях форму и размеры проецируемой фигуры.

В машиностроении, для того чтобы иметь возможность по чертежу судить о форме и размерах изображаемых деталей пользуются не двумя, а несколькими плоскостями проекций, как правило, тремя. Эти три взаимно ортогональные плоскости носят названия: П1 - горизонтальная, П2 - фронтальная и П3 - профильная плоскость проекций. На рисунке 6 показано построение проекций точки в этой системе плоскостей проекций.

 

 

Рисунок 6

Рисунок 6 представляет пространственное изображение точки А и плоскостей проекций, но в инженерной практике пользоваться такими изображениями не всегда удобно. Поэтому применяется плоский чертёж, на котором совмещены все три плоскости и который носит название Эпюр Монжа. Образуется он следующим образом: горизонтальная плоскость П1 поворачивается вокруг оси Х на 90 градусов вниз до совмещения с фронтальной плоскостью, а профильная поворачивается вокруг оси Z на 90 градусов вправо. В результате получим плоское изображение всех трёх плоскостей проекций (рисунок 7). Этот чертёж называется эпюром Монжа или комплексным чертежом.

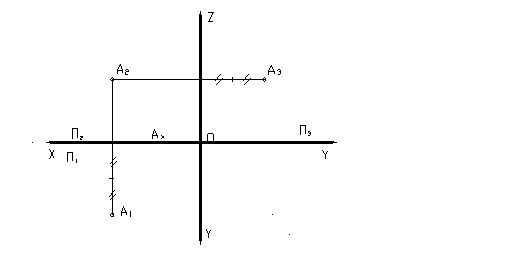
Рисунок 7

 

Построим проекции точки А, изображённой на рисунке 6, на эпюре Монжа. Для этого отложим по оси X (рис.7) координату точки А по оси Х – расстояние Ах. Затем из этой точки восстановим перпендикуляры к оси Х на плоскости П2 и П1.

Вверх, на плоскость П2, отложим высоту точки А или её координату по оси Z, а вниз, на плоскость П1, откладываем глубину точки два раза. Это искажение по оси У получается из-за того, что ось У повернулась на 45 градусов по сравнению с пространственным изображением. Для того чтобы построить профильную проекцию точки А, из её фронтальной проекции А2 проводим перпендикуляр к оси Z и откладываем на нём от оси Z глубину точки или её координату по оси У. Полученные три проекции точки А(А1, А2, А3) дают полное представление о положении точки в пространстве. Этот чертёж называется комплексным чертежом точки. Линии, соединяющие проекции точки, называются линиями связи.

 

1. Что изучает начертательная геометрия ?

2. Что называется чертежом ?

3. В чем отличие начертательной геометрии от инженерной графики ?

4. Назовите основные этапы развития геометрии.

5. Какие специальные символы существуют для обозначения параллельности, перпендикулярности, пересечения, скрещивания? Какие обозначения вы знаете, кроме этих ?

6. В чем сущность центрального проецирования ?

7. Как образуется проекция точки при параллельном проецировании ?

8. Назовите основные плоскости проекций.

9. Что такое эпюр Монжа ? Как он образуется ?