Группированная выборка
Пример.
При проведении 20 серий из 10 бросков игральной кости число выпадений шести очков оказалось равным 1,1,4,0,1,2,1,2,2,0,5,3,3,1,0,2,2,3,4,1.Составим вариационный ряд: 0,1,2,3,4,5. Статистический ряд для абсолютных и относительных частот имеет вид:
| xi | ||||||
| ni | ||||||
| wi | 0,15 | 0,3 | 0,25 | ,15 | 0,1 | 0,05 |
Если в статистическом распределении вместо частот (относительных частот) указать накопленные частоты (относительные накопленные частоты), то такой ряд распределения называют кумулятивным.
Накопленная частота представляет собой сумму частот всех значений, от x1 до xi.: Fi = ∑ij=1 nj. По накопленной частоте можно определить, для какой части выборки значения переменной X не превосходят значения xi.
Если исследуется некоторый непрерывный признак, то вариационный ряд может состоять из очень большого количества чисел. В этом случае удобнее использовать группированную выборку. Для ее получения интервал, в котором заключены все наблюдаемые значения признака, разбивают на несколько равных частичных интервалов длиной h, а затем находят для каждого частичного интервала ni – сумму частот вариант, попавших в i-й интервал. Составленная по этим результатам таблица называется группированным статистическим рядом:
| Номера интервалов | … | |||
| Границы интервалов | (a, a + h) | (a + h, a + 2h) | … | (b – h, b) |
| Сумма частот вариант, попавших в интервал | n1 | n2 | … | nk |
Для получения группированной выборки нужно:
1) Опредеить минимальное и максимальное значение вариант и рассчитываем размах вариационного ряда по формуле: R=Xmax - Xmin
2) Рассчитать число классов по формуле Стерджеса: 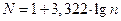
3) Рассчитать интервал каждого класса по формуле: 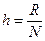
4) Составить таблицу границ классов.
5) Рассчитать среднее значение каждого класса.
Пример:
Построить графики вариационного ряда 20 исследуемых по показателям результатов тестирования прыжка в высоту, если данные выборки таковы: xi, см ~ 185, 170, 190, 170, 190, 178, 188, 175, 192, 178, 176, 180, 185, 176, 180, 192, 190, 190, 192, 194.
Решение:
1) Определяем минимальное и максимальное значение вариант и рассчитываем размах вариационного ряда: R=194-170=24 см
2) Рассчитываем число классов по формуле Стерджеса: N=1+3,31 lg1,301=5,30631»5
3) Рассчитываем интервал каждого класса: 
4) Составляем таблицу границ классов.
| интервал | 170-174,8 | 174,8-179,6см | 179,6-184,4см | 184,4 -189,2 | 189,2-194 |
| Частота класса | |||||
| Накопленная частота класса Fi | |||||
| Среднее значение класса | 172,4 см | 177,2 см | 182 см | 186,8 см | 191,6 см |
Группированная форма представления случайной величины не содержит информации о каждом элементе выборки. При этом часто в качестве значения случайной величины на каждом интервале принимается его середина.
От негруппированной выборки всегда можно перейти к группированной, но не наоборот. Необходимо помнить, что переход к группированной форме представления выборки сопряжен с потерей информации об исследуемом объекте, процессе или явлении.