Собственные значения и собственные векторы матрицы

Определение: Ненулевой вектор называется собственным вектором матрицы А, если существует такое число l, что выполняется равенство:

A.

Число l называется собственным значениемматрицы А, соответствующим вектору .

Определение: Матрица 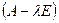называется характеристической матрицей матрицы 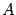, многочлен называется характеристическим многочленом матрицы 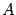, уравнение называется характеристическим уравнением матрицы .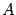

Пример. Найдите собственные числа и собственные векторы матрицы

.

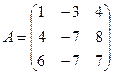Решение. Составляем характеристическую матрицу :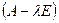

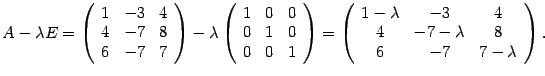
Находим характеристический многочлен

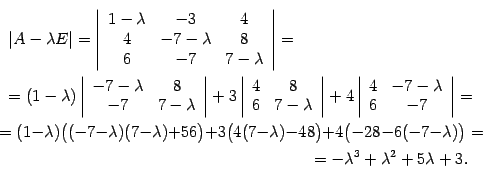
Решим характеристическое уравнение

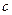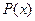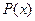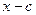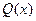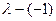Подбором находим, что один корень уравнения равен -1. По теореме Безу, которая говорит, что если число является корнем многочлена , то многочлен делится на разность , то есть , где - многочлен. В соответствии с этой теоремой многочлен должен делиться на . Выделим в характеристическом многочлене этот множитель :

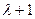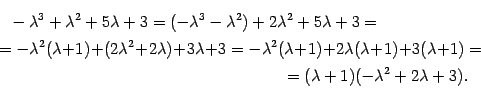
Находим корни трехчлена 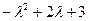. Они равны -1 и 3. Таким образом,

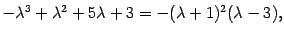
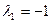- корень кратности 2, - корень. Итак, собственные числа матриц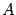ы равны , .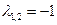

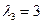Найдем соответствующие им собственные векторы.

Пусть 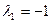, тогда для собственного вектора получаем матричное уравнение

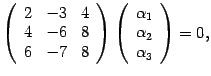
что соответствует системе уравнений

Решаем ее методом Гаусса. Выписываем расширенную матрицу системы

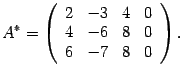
Первую строку, умноженную на числа -2 и -3, прибавляем соответственно ко второй и третьей строкам

Меняем местами вторую и третью строки

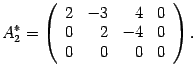
Возвращаемся к системе уравнений

–

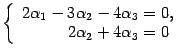
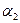Переменные и оставляем в левой части, а переменную переносим в правую часть

Полагаем 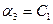, находим , при .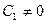

Итак, собственному числу 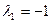соответствует собственный вектор .

Пусть 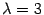, тогда для собственного вектора получаем матричное уравнение

что соответствует системе уравнений

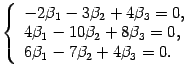
Решаем ее методом Гаусса. Выписываем расширенную матрицу

Первую строку умножаем на числа 2 и 3 и прибавляем соответственно ко второй и третьей строкам

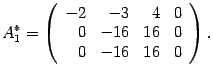
Вторую строку умножаем на -1 и прибавляем к третьей

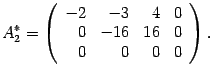
Возвращаемся к системе уравнений

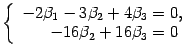
Переменные и оставляем в левой части, а переменную 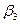переносим в правую часть

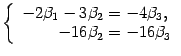
Полагаем 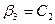, находим , .

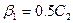Итак, собственному числу соответствует собственный вектор .

Чтобы избавиться от дроби, умножим собственный вектор на 2, получим собственный вектор с тем же самым собственным числом. В итоге собственному числу соответствует собственный вектор .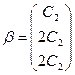

Ответ: Собственные числа: 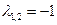, , соответствующие собственные векторы: , .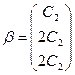