Случай 2.
Лекция. Однородные системы линейных уравнений
В матричной форме однородная линейная система уравнений имеет следующий вид
АХ = Ô.
Например,

Очевидно, что однородная система всегда совместна, т.к. RgA=Rg(A,Ô) или хотя бы потому, что она всегда имеет нулевое решение х1=х2=...=хn=0, которое называется тривиальным. Поэтому метод Гауcса применим к однородным системам без каких-либо изменений. При этом возможны следующие случаи:
Случай 1.
Rg A = nи система имеет единственное тривиальное (нулевое) решение.
Rg A =r и r < nи система имеет бесчисленное множество решений, включая тривиальное.
В этом случае, если придать свободным неизвестным n -r наборов значений:
1) хr+1 = 1 , хr+2 = 0 ,... хn-1 = 0 , хn = 0 ,
2) хr+1 = 0 , хr+2 = 1 ,... хn-1 = 0 , хn = 0 ,
..............................................................
n-r) хr+1 = 0 , хr+2 = 0 ,... хn-1 = 0 , хn = 1
и для каждого набора свободных неизвестных найти значения базисных неизвестных х1 , х2 , ..., хr , то можно выписать n - r частных решений системы

Полученная таким образом система (так называемых линейно независимых, их число равно n-r) решений называется фундаментальной системой решений однородной системы уравнений.
Справедливы следующие теоремы:
Теорема 1. Общее решениеоднородной системы имеет вид

где с1 ,с2 ,..., сn-r - произвольные числа.
Теорема 2.
Общее решение неоднородной совместной системы линейных уравнений равно сумме общего решения соответствующей ей системы однородных уравнений и произвольного частного решения неоднородной системы.
Таким образом, с учетом рассмотренного выше, можно записать следующую общую схему решения систем линейных уравнений.
Общая схема решения систем линейных уравнений
Пример 19
Пример 1.
Решить систему
 (*)
(*)
Решение.
Дана неоднородная линейная система из 4-х уравнений с 4-мя неизвестными.
1) Определим, совместна или нет система (*). Вычисляем для этого Rg(A,B) и RgA.
(А,В) =  ~
~ ~
~ = (A',B')
= (A',B')
(привели матрицу (А,В) к ступенчатой форме).
Þ Rg(A,B) = 2, RgA=2 Þ RgA= Rg(A,B) Þ система (*) совместна. Т.к. Rg A < n (n = 4) Þ система имеет бесчисленное множество решений.
2) Найдем все решения системы (*). Для этого перейдем к следующей эквивалентной системе
 (**)
(**)
где
х1 и х2 - базисные неизвестные,
х3 и х4 -свободные неизвестные.
От системы (**) перейдем к другой эквивалентной системе
 (***)
(***)
Решая систему (***) , как систему из 2-х уравнений с 2-мя неизвестными х1 и х2 , найдем их. Из последнего уравнения имеем
х2 = 
Тогда из первого уравнения найдем
х1= -3х3+х4-2х2 = -3х3 + х4 +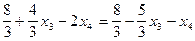
Т.к. х3 и х4 - свободные неизвестные, то можно считать х3 = a, х4 = b.
Тогда общее решение системы (***), а значит и (*) имеет вид
х1= х2=
х2= х3 = a, х4= b или
х3 = a, х4= b или
Х= =
= 
 +
+  b +
b + 
 +
+ (*)
(*)
Проверка общего решения(по исходной системе).

Þ общее решение найдено верно.
Ответ. 
 х3 = a, х4 = b4
х3 = a, х4 = b4
3Пример 2.
Найти все базисные решения предыдущего примера.