Элементы квантовой статистики
Лекция № 12
Решение
2.7.1 Для базисного периода
2.7.1.1 Число оборотов запасов (Кр и В из 2.3) Коб=КрВ/Зср, ; Зср=(Зн+Зк)/2 = (30+12)/2=21 млн. руб. ; Коб=70,638/2111=3,36 об./год
2.7.1.2. Период оборотов запасов в годах tг = 1/Коб= 1/3,36=0,297 лет
2.7.1.3 Период оборота в сутках tоб=365*tг=0,297*365=108,405 сут.
2.7.1.4 Обеспеченность запасами tоз=Зн/А = 30/0,2 = 150 сут.
2.7.2 Для отчететного периода (аналогично):
2.7.2.1 Число оборотов запасов Зср= (35+19)/2 = 27 млн. руб. ; Коб=80,373/27=2,977 об./год.
2.7.2.2 Период оборотов запасов в годах tг = 1/2,977=0,336 лет
2.7.2.3 Период оборота в сутках tоб=0,336*365=122,64 сут.
2.7.2.4 Обеспеченность запасами tоз= 35/0,21 = 166,67 сут.
2.7.3.1 Абсолютное изменение показателей
I1=2,977-3,36=-0,383 об./год;
I2=0,336-0,297=0,039 лет;
I3=122,64-108,405=14,235 сут.;
I4=166,67-150=16,67 сут.
2.7.3.2 Относительное изменение показателей
I1=2,977/3,36=0,886 (уменьш. на 11,4%);
I2=0,336/0,297=1,132 (увелич. на 13,2%);
I3=122,64/108,405=1,132 (увелич. на 13,2%);
I4=166,67/150=1,111 (увелич. на 11,1%)
Распределение Гиббса и учет неразличимости микрочастиц
В классической механике частицы одинаковой природы (например, электроны) можно различать. Пронумеровав их в некоторый момент времени t0, можно следить за их движением по траектории, и в момент времени t определить какой номер был присвоен той или иной частице.
В квантовой механике положение иное. В силу принципа неопределенности понятие траектории частицы утрачивает смысл. Поэтому частицы одинаковой природы становятся неразличимы. Это утверждение носит название принципа неразличимости (или тождественности) одинаковых частиц.
Пусть мы имеем систему, состоящую из двух тождественных частиц. Обозначим через ε1 и ε2 совокупность координат и проекции спина частиц. Так как частицы неразличимы, перестановка индексов при ε не должна изменять физических свойств системы, то есть изменять квадрат модуля волновой функции. Следовательно,
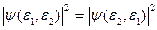
Здесь возможны два случая:
- функция ψ симметрична к переменным ε1 и ε2
и 
- антисимметричная функция.
Частицы с нулевым или целым спином описываются симметричными волновыми функциями, а с полуцелым спином – антисимметричными функциями.
| Частицы с нулевым и целым cпином Могут находиться в одинаковом состоянии в неограниченном количестве (коллективность). Такие частицы подчиняются статистике, разработанной Бозе и Эйнштейном, и называются БОЗОНАМИ (пример: фотоны, π - – и κ- мезоны). | Частицы с полуцелым спином Могут находиться в квантовых состояниях только поодиночке (индивидуалисты). Такие частицы подчиняются статистике, разработанной Ферми и Дираком, и называются ФЕРМИОНАМИ (пример: электроны, протоны и нейтроны). |
Одной из основных задач статистической физики является нахождение закона распределения частиц по разным квантовым состояниям.
Пусть имеется система тождественных частиц, каждая из которых может находиться в состояниях с фиксированными значениями энергии ε1 и ε2 … Каждому значению энергии соответствует одно состояние, что характеризуется средним числом частиц, обладающих данной энергией n1, n2… или их еще называют числом заполнения объема, где они находятся.
При больших числах заполнения закон распределения для фермионов и бозонов оказывается неодинаковым.
Швейцарский физик Вольфганг Паули сформулировал принцип, согласно которому в одной и той же квантовой системе не может быть двух частиц с полуцелым спином, обладающих одинаковой совокупностью квантовых чисел. К таким частицам относится электрон.
Состояние электрона в атоме характеризуется четырьмя квантовыми числами: главным n, азимутальным l , магнитным mi и спиновым ms:
n = 1,2,3…;
l =0,1,2… (n -1);
mi =0,±1,…. ,± l;
ms = ½, - ½ .
В основном (невозбужденном) состоянии атома электроны должны располагаться на самых низких энергетических уровнях. Применительно к электронам принцип Паули гласит:
В одном и том же атоме не может быть двух электронов, обладающих одинаковой совокупностью квантовых чисел.
В состояниях с данным значением n в атоме может быть не более 2n2 электронов.
Совокупность электронов, имеющих одинаковые значения квантового числа n, образует оболочку.
В соответствии со значением n оболочкам дают следующие обозначения:
| n | …. | |||||||
| Обозначение | K | L | M | N | O | P | Q | …. |
Принцип Паули дает объяснение периодической повторяемости свойств атомов, исходя из электронных конфигураций атома.
Рассмотрим систему N тождественных молекул, помещенных в закрытом сосуде. Будем считать молекулы материальными точками и считать, что состояние отдельной молекулы определяется ее координатами X, Y, Z и импульсом Рх , Ру , Рz . При этом допускаются только дискретные состояния системы. Промежуточных состояний не существует. Они характеризуются определенными значениями энергии ε1 и ε2 .
Кроме этого, будем считать, что частицы принципиально различимы, хотя могут быть и абсолютно тождественными. Это положение лежит в основе так называемой статистики Больцмана.
Закон распределения частиц по квантовым состояниям определяется формулой
(1) 
; 
Таким образом, если мы имеем две частицы, то распределение энергии в них может быть следующее:
2 частицы → обе ε1
2 частицы → обе ε2
первая в ε1 , вторая в ε2
первая в ε2 , вторая в ε1.
То есть, имеем 4 возможных квантовых состояния. Из формулы (1) следует, что равновесное состояние системы не зависит от того, какой она окружена, а зависит от температуры среды.
Из этой формулы получается формула Вина для равновесного теплового излучения справедливая только для высоких частот излучения.
Можно изменить задачу: задаваясь температурой, подсчитать вероятность того, что система окажется в заданном квантовом состоянии. Формула (1) оказывается применимой и в этом случае; для этой задачи она называется каноническим распределением Гиббса. Это распределение представляет собой наиболее общую и удобную основу для построения статистической механики.
Статистика Больцмана является приближенным предельным случаем, в который переходят статистики Ферми-Дирака и Бозе-Эйнштейна.
Статистика Бозе-Эйнштейна. Фотонный газ
Во всех трех статистиках (Больцмана, Бозе-Эйнштейна и Ферми-Дирака) допустимые состояния системы считаются равновероятными. Статистика Больцмана стоит на точке зрения принципиальной различимости частиц даже тогда, когда они абсолютно тождественны. Если частица А находится в состоянии I, а частица В - в состоянии II, то получится новое микросостояние, когда обе частицы поменяются местами.
Квантовые статистики Бозе-Эйнштейна и Ферми-Дирака наоборот считают, что при такой перестановке никаких изменений не произойдет, получится такое же микросостояние. Обе эти статистики стоят на точке зрения принципиальной неразличимости тождественных частиц.
В статистике Ферми-Дирака считают, что в каждом квантовом состоянии может находиться не более одной частицы.
В статистике Бозе-Эйнштейна считают, что в каждом квантовом состоянии может находиться любое количество частиц.
Закон распределения частиц по квантовым состояниям в статистике Бозе-Эйнштейна определяется формулой
При малых числах заполнения экспонента в знаменателе много больше единицы, поэтому единицей в знаменателе можно пренебречь и получить распределение, как в статистике Больцмана.
Если мы имеем две частицы, то распределение энергии в них может быть следующее:
2 частицы → обе ε1
2 частицы → обе ε2
Одна в ε1, другая в ε2 (если поменять их местами, будет все равно прежнее состояние).
То есть, имеем три возможных квантовых состояния системы. Спин фотона равен единице. Следовательно, фотоны являются бозонами. Фотоны не взаимодействуют между собой. Поэтому излучение, находящееся в равновесии со стенками полости, в которой оно заключено, можно рассматривать как фотонный газ. Стенки полости непрерывно излучают и поглощают фотоны, поэтому общее число фотонов определяется объемом полости и температурой ее стенок. Их число не фиксировано и, следовательно, законы сохранения на них не распространяются. Фотонный газ, находящийся в равновесном состоянии является системой с одной степенью свободы. Среднее число фотонов
,
где μ – термодинамический потенциал. Для равновесного состояния μ=0. Следовательно, для фотонов газа среднее число фотонов с данной энергией U определяется, как
.
Из этой формулы получается формула Планка для равновесного теплового излучения.
Статистика Ферми – Дирака. Фононный газ.
Согласно этой статистике частицы с полуцелым спином могут находиться в квантовых состояниях только поодиночке.
Закон распределения частиц по квантовым состояниям определяется формулой 
.
Таким образом, если мы имеем две частицы, то распределение энергии в них может быть следующее:
1ая частица → ε1 ;
2ая частица → ε2 ; т.е. имеем только одно возможное квантовое состояние.
Исходя из идентичности выражений закона распределения частиц по кванто-
вым состояниям и среднего числа фотонов с данной энергией, имеем следующий график
При Т=0 частицы заполняют все квантовые состояния 
, а так как μ=0, то имеем полное выражение колебаний частиц.
При Т>0 энергия колебания частоты ωi слагается из порций 
, которые можно назвать квантами звука. Это дает основание сопоставить нормальному колебанию квазичастицу, называемую ФОНОНОМ.
Если квантом света является фотон, то квантом звука – фонон.
Фонон обладает энергией и импульсом. Однако, в отличие от обычных частиц (электронов, фотонов, протонов) фонон не может возникнуть в вакууме. Для своего возникновения фонон нуждается в среде. Подобного рода частицы называются квазичастицами.
Импульс фонона обладает следующими свойствами:
ü При взаимодействии фононов он передается дискретными порциями и, следовательно, не сохраняется;
ü Возможно возбуждение неограниченного числа одинаковых фононов.
Таким образом, колебания можно представить, как фононный газ, подобно тому, как электромагнитное излучение можно представить, как фотонный газ, заполняющий полость. Формально оба представления весьма схожи: и фотоны, и фононы подчиняются одной и той же статистике. Однако между фотонами и фононами имеется существенное различие: в то время, как фотоны являются истинными частицами, фононы являются квазичастицами.
Результаты изложенного материала кратко можно свести в следующую таблицу:
| Виды статистики | Распределение частиц по энергиям | Число возможных состояний | Закон распределения |
| Классическая статистика Больцмана | 2 частицы в ε1; 2 частицы в ε2; 1ая частица в ε1, 2ая частица в ε2; 1ая частица в ε2, 2ая частица в ε1. | 
| |
| Квантовая статистика Бозе-Эйнштейна | 2 частицы в ε1; 2 частицы в ε2; одна частица в ε1, другая частица в ε2. | 
| |
| Квантовая статистика Ферми-Дирака | одна частица в ε1, другая частица в ε2. | 
|