Пример 5.

Рис.4.14

 

Из рисунка следует:

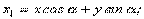
Теперь определим моменты инерции относительно осей х₁ и у₁:

или . (14)

Аналогично:

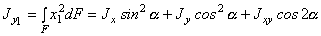. (15)

(16)

Сложив почленно уравнения (14), (15), получим:

,

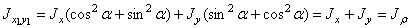т.е. сумма моментов инерции относительно любых взаимно перпендикулярных осей остается постоянной и не изменяется при повороте системы координат.

Найти моменты инерции прямоугольника (рис.4.15) относительно осей и и центробежный момент его относительно тех же осей.

Рис.4.15