Треугольник

Рис. 4.8

Прямоугольник

Определим моменты инерции относительно осей, совпадающих со сторонами, и относительно центральных осей.

По определению .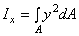

 

Элемент площади равен dA = bdy,

следовательно .

По формуле 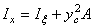, откуда, учитывая что А = bh, y_c = 0,5h, находим

.

Аналогично получим и .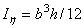

Момент инерции относительно оси х, cовпадающей с основанием,

.

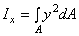Но dA = b(y)dy, b(y) = (b/h)(h-y).

Cледовательно,

.