Лекция 9.1. Дифференциальные уравнения первого порядка, их виды и методы решения
ТЕМА 9. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
План:
1. Понятие дифференциального уравнения и его решения.
2. Дифференциальное уравнение первого порядка. Задача Коши.
3. Основные виды дифференциальных уравнений первого порядка.
При решении задач математики, физики, химии и других наук часто используют математические модели в виде уравнений, связывающих в качестве неизвестной некоторую функцию  и ее производные различных порядков. Одно из наиболее простых дифференциальных уравнений – уравнение вида
и ее производные различных порядков. Одно из наиболее простых дифференциальных уравнений – уравнение вида 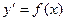 , лежит в основе задачи интегрального исчисления. Очевидно, что решение этого уравнения будет функция, определяемая через интеграл
, лежит в основе задачи интегрального исчисления. Очевидно, что решение этого уравнения будет функция, определяемая через интеграл  .
.
Следующие примеры позволяют лучше понять, как различные задачи формулируются на языке дифференциальных уравнений.
Пример 8.(Радиоактивный распад). Закон распада некоторых радиоактивных веществ состоит в том, что скорость распада пропорциональна наличному количеству этого вещества. Если x – количество вещества в некоторый момент времени t, то этот закон можно записать так:
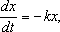
где 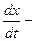 скорость распада, а k – некоторая положительная постоянная, характеризующая данное вещество. (Знак «-» в правой части указывает на то, что x убывает со временем; знак «+» означает, что x возрастает со временем).
скорость распада, а k – некоторая положительная постоянная, характеризующая данное вещество. (Знак «-» в правой части указывает на то, что x убывает со временем; знак «+» означает, что x возрастает со временем).
Пример. (Математическая модель демографического процесса). Из статистических данных известно, сто для рассматриваемого региона число новорожденных и число умерших за единицу времени пропорциональны численности населения с коэффициентами пропорциональности 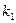 и
и 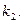 Обозначим через
Обозначим через 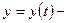 число жителей региона в момент времени
число жителей региона в момент времени 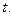 Прирост населения
Прирост населения 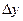 за время
за время 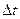 равен разности между родившихся и умерших за это время, то есть
равен разности между родившихся и умерших за это время, то есть 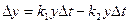 или
или 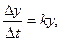 где
где 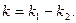 Переходя к пределу при
Переходя к пределу при 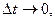 получаем уравнение
получаем уравнение 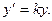 Общим решением этого уравнения будет функция
Общим решением этого уравнения будет функция 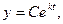 где
где 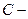 произвольная постоянная, которую можно определить исходя из численности населения в начальный момент времени. Функцию
произвольная постоянная, которую можно определить исходя из численности населения в начальный момент времени. Функцию 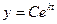 называют законом изменения численности населения с течением времени.
называют законом изменения численности населения с течением времени.
После того, как задача записана на языке дифференциальных уравнений, следует попытаться их решить, т.е. найти величины, скорости изменения которых входят в уравнения.