Ряды Фурье

Допустим, что функция f(x) задана в интервале (-p, p). Представим её в виде тригонометрического ряда, так же как мы раньше записывали функцию в виде степенного ряда:

. (18)

Задача состоит в нахождении коэффициентов ряда для данной функции. И если для отыскания коэффициентов ряда Тейлора нам пришлось дифференцировать ряд, то сейчас придётся интегрировать.

Тригонометрические ряды являются равномерно сходящимися, и, следовательно, их можно почленно интегрировать. Поэтому с учётом формул (13), (14) после интегрирования (18) получим:

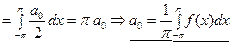. (19)

Чтобы найти а_n, умножим равенство (18) на и затем его проинтегрируем:

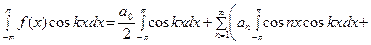
. (20)

При выводе этой формулы были использованы формулы (14), (15), (16).

Для нахождения b_n умножим равенство (18) на 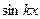и затем его проинтегрируем:

. (21)

При выводе этой формулы были использованы формулы (13), (15), (17).

Таким образом, вычислив по формулам (19)-(21) коэффициенты тригонометрического ряда (коэффициенты Фурье), мы можем написать ряд Фурье функции f(х):

. (22)

Если ряд конечен, т.е. обрывается на каком-то члене, то он называется многочленом Фурье.

Пусть функция f(х) задана в интервале (-p, p). Тогда могут осуществиться два варианта: 1) f(p) = f(-p) и 2) f(p) ¹ f(-p). Если продолжить эту функцию на всю числовую ось периодически с периодом 2p, то в первом случае функция окажется непрерывной , а во втором - в точках будут разрывы первого рода.

Функция называется гладкой в замкнутом интервале, если в этом интервале она непрерывна вместе со своей первой производной. Функция называется кусочно-гладкой в замкнутом интервале, если его можно разбить на конечное число частично-замкнутых интервалов, в каждом из которых функция гладкая.

Теорема Дирихле. Если функция f(х) кусочно-гладкая в интервале (-p, p), то её ряд Фурье сходится к функции f(х) во всех точках интервала, в которых она непрерывна. В точках разрыва функция сходится к среднему арифметическому её предельных значений слева и справа, т.е. к значению , где х₀ - точка разрыва первого рода. В обеих граничных точках интервала сумма ряда равна среднему арифметическому предельных значений функции при стремлении независимой переменной к этим точкам изнутри интервала: .

Условия, при которых выполняется теорема Дирихле, могут быть сформулированы в виде условий Дирихле: функция должна иметь в интервале (-p, p) конечное число точек разрыва первого рода (или быть непрерывной) и конечное число точек экстремума (или не иметь их вовсе).

Если функция задана не в интервале (-p, p), а на произвольном симметричном интервале (-l, l), то её тоже можно представить в виде ряда Фурье. Для этого вводят новую переменную , и при этом функция от t будет задана в интервале (-p, p). Её уже можно записать как стандартный ряд Фурье. А заданная функция предстанет в виде

, где

, n = 0, 1, 2, …;

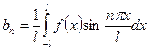, n = 1, 2, 3 ….

Если функция чётная, то её ряд Фурье должен содержать тоже только чётные функции (это константа и косинусы), а значит, ряд имеет вид

где (23)

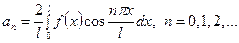Если функция нечётная, то все коэффициенты 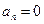, так как нечётными являются только синусы, и её ряд Фурье такой:

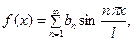где (24)

Если задана в интервале [0, l), то её можно продолжить в соседний интервал (-l, 0) двумя способами. Если продолжить чётным образом, то разложение в ряд Фурье будет иметь вид (23). Если же продолжение нечётное, то будет ряд по синусам (24).

Пример 1.Разложить функцию в ряд Фурье в интервале .

Решение. Отметим, что функция чётная, график её симметричен относительно оси OY (рис. 4). Продолжив её на всю ось ОХ, получим непрерывную, периодическую функцию с периодом 2p, удовлетворяющую условиям Дирихле.

Рис. 4. График ряда Фурье функции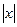

Воспользовавшись чётностью функции, интегралы (19) и (20) вычисляем как удвоенные интегралы в пределах (0, p):

Заметим, что последний интеграл был вычислен методом интегрирования по частям, а все коэффициенты , так как функция чётная.

Получим ряд

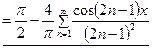. (25)

Равенство верно при всех х из промежутка , так как функция непрерывна на промежутке и на концах интервала имеет одинаковые значения, а по теореме Дирихле в точках непрерывности функции сумма ряда совпадает с самой функцией.

Подставим х = 0 в формулу (25):

Таким образом, с помощью ряда Фурье нам удалось просуммировать бесконечную сумму обратных квадратов нечётных чисел!

Зная этот результат, теперь легко найти и сумму S обратных квадратов всех натуральных чисел:

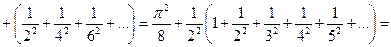
А если в формуле (25) взять х = p/4, то получится ещё более интересный знакопеременный ряд, сумму которого позволяет найти ряд Фурье:

В этом ряде после единицы следуют по очереди два минуса, затем два плюса и т.д.

Из этих примеров видно, какая есть дополнительная польза от рядов Фурье.

Пример 2.Разложить функцию 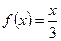в ряд Фурье в интервале .

Решение. Продолжим эту функцию нечётным образом на отрицательные х (рис. 5) .

Рис. 5. График ряда Фурье функции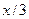

Для нечётной функции ряд Фурье следует вычислять по формуле (24), где :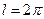

Этот интеграл был взят «по частям». В результате мы получили разложение заданной функции в ряд Фурье:

, (26)

который сходится во всех точках интервала к данной функции. В точке х = 2p сумма ряда равна 0, как это и следует из теоремы Дирихле (на рис. 5 видно, что полусумма значений изображённой там функции слева и справа от х = 2p равна нулю).

Подставив в формулу (26) х = p, получим ещё один числовой ряд:

т.е. знакочередующийся ряд, составленный из обратных величин нечётных чисел равен p / 4.

Пример 3.Разложить в ряд Фурье по косинусам функцию

. (27)

Решение. Продолжим данную функцию симметрично относительно оси ординат. Так как функция получилась чётной на промежутке , то её ряд Фурье будет содержать только косинусы.

Рис. 6. График ряда Фурье функции (27)

Найдём коэффициенты Фурье а_n:

Так как = 0 при чётном n и при нечётном n, то .

В результате получилось разложение функции (27) в ряд

, (28)

который во всех точках сходится к самой функции f(x), кроме точки разрыва первого рода . В этой точке, так как , ряд равен , т.е. полусумме значений функции справа и слева от т. .

Взяв в формуле (28) и учитывая, что f() = 1, получим новый экзотический ряд:

В этом знакопеременном ряде два плюса чередуются с двумя минусами, а модули членов ряда равны обратным величинам нечётных чисел.

В заключение обратим внимание читателя на сущность рядов Фурье. Анализируя полученные нами формулы (25), (26) и (28), видим, что каждый член ряда является простой гармоникой периодической функции f(x). Каждая гармоника имеет свою амплитуду, убывающую с ростом номера гармоники. Набор амплитуд этих гармоник называется спектром функции f(x).