Тригонометрические ряды
План лекции
7.1. Тригонометрические ряды
7.2. Ряды Фурье
7.3. Ряд Фурье в комплексной форме
7.1.1. Общие представления
Поведение многих механических, электрических и других колебательных процессов при отсутствии потерь описывается тригонометрической функцией
 ,
,
где А0 - амплитуда колебаний,  - фаза, w0 - собственная частота колебаний, j0 - начальная фаза колебаний. Такое колебание называется простой гармоникой с периодом
- фаза, w0 - собственная частота колебаний, j0 - начальная фаза колебаний. Такое колебание называется простой гармоникой с периодом  . Если кроме собственных колебаний объект участвует ещё в движении под действием внешней периодической силы с циклической частотой w1, то его поведение будет описываться уже такой функцией
. Если кроме собственных колебаний объект участвует ещё в движении под действием внешней периодической силы с циклической частотой w1, то его поведение будет описываться уже такой функцией
 .
.
Это результирующее колебание будет периодическим, если у двух колебаний есть общий период Т, т.е. если найдутся такие целые числа т0 и т1 такие, что  , где
, где  . Другими словами, частоты для этого должны быть соизмеримы:
. Другими словами, частоты для этого должны быть соизмеримы:  .
.
Если на объект действуют n периодических сил, то колебание будет периодическим, если выполняются равенства  .
.
Отсюда следует вывод, что произвольное периодическое колебание можно представить как конечную или бесконечную сумму простых гармоник. Значит, любую периодическую функцию можно записать в виде тригонометрического ряда, состоящего из косинусов и синусов.
Функциональный ряд вида


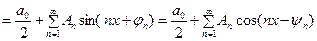 ,
,
где  ,
,  ,
, 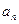 и
и  – постоянные числа называется тригонометрическим рядом. Заметим, что функции
– постоянные числа называется тригонометрическим рядом. Заметим, что функции  и
и 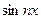 имеют период 2p/n, а значит, общим периодом для всех функций в тригонометрическом ряде является 2p. Разложение функций в тригонометрические ряды называется гармоническим анализом, так как этим достигается представление какого-либо сложного периодического процесса в виде простых гармонических колебаний.
имеют период 2p/n, а значит, общим периодом для всех функций в тригонометрическом ряде является 2p. Разложение функций в тригонометрические ряды называется гармоническим анализом, так как этим достигается представление какого-либо сложного периодического процесса в виде простых гармонических колебаний.
7.1.2. Ортогональная система функций
Система функций  называется ортогональной в интервале (а, b), если интеграл от произведения любых двух различных функций системы равен нулю:
называется ортогональной в интервале (а, b), если интеграл от произведения любых двух различных функций системы равен нулю:
 . (12)
. (12)
Система функций называется ортонормированной, если
 .
.
Оказывается, тригонометрические функции образуют ортогональную систему функций в интервале (-p, p). Покажем это, вычислив ряд интегралов.
1)  ; (13)
; (13)
2) ; (14)
; (14)
3) ; (15)
; (15)
4) (16)
(16)
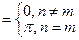 ;
;
5) (17)
(17)
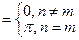 .
.
Как видим условие (12) выполняется, поэтому тригонометрические функции cos nx и sin mx являются ортогональными. А ортонормированную систему образуют функции  и
и  .
.