Вторая теорема двойственности
Пусть даны две взаимно двойственные задачи. Если каждую из этих задач решать симплексным методом, то необходимо привести их к каноническому виду, для чего в систему ограничений задачи I (в краткой записи 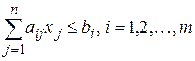 ) следует ввести т неотрицательных переменных
) следует ввести т неотрицательных переменных  , а в систему ограничений задачи II (
, а в систему ограничений задачи II (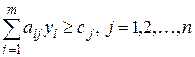 ) – n неотрицательных переменных
) – n неотрицательных переменных  , где
, где  – номер неравенства, в которое введена дополнительная переменная
– номер неравенства, в которое введена дополнительная переменная  .
.
Системы ограничений каждой из взаимно двойственных задач примут вид:
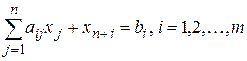
 .
.
Установим соответствие между первоначальными переменными одной из двойственных задач и дополнительными переменными другой задачи (таблица).
| Переменные исходной задачи I | |
| Первоначальные | Дополнительные |
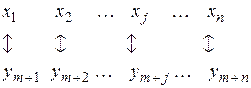
| 
|
| Дополнительные | Первоначальные |
| Переменные исходной задачи II |
Теорема. Положительным (ненулевым) компонентам оптимального решения одной из взаимно двойственных задач соответствуют нулевые компоненты оптимального решения другой задачи, т.е. для любых 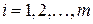 u
u 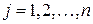 : если
: если  , то
, то 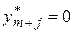 ; если
; если  , то
, то 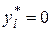 , и аналогично,
, и аналогично,
если 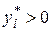 , то
, то 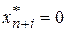 ; если
; если 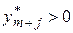 , то
, то 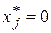 .
.
Из данной теоремы следует важный вывод о том, что введенное соответствие между переменными взаимно двойственных задач при достижении оптимума (т.е. на последнем шаге решения каждой задачи симплексным методом) представляет соответствие междуосновными (как правило, не равными нулю) переменными одной из двойственных задач инеосновными (равными нулю) переменными другой задачи, когда они образуют допустимые базисные решения.
Вторая теорема двойственности. Компоненты оптимального решения двойственной задачи равны абсолютным значениям коэффициентов при соответствующих переменных линейной функции исходной задачи, выраженной через неосновные переменные ее оптимального решения.
Замечание. Если в одной из взаимно двойственных задач нарушается единственность оптимального решения, то оптимальное решение двойственной задачи вырожденное. Это связано с тем, что при нарушении единственности оптимального решения исходной задачи в выражении линейной функции ее оптимального решения через неосновные переменные отсутствует хотя бы одна из основных переменных.