Разложение функций в степенные ряды

О функции, которая представлена в виде некоторого степенного ряда, говорят, что она разложена в степенной ряд. Представление функций в виде степенного ряда используется в приближённых вычислениях и при решении дифференциальных уравнений.

Разложение одной функции мы уже имеем: это формула (5), записанная в обратном порядке

, . (6)

Из этой формулы можно получить ещё одно разложение, заменив там х на (-х):

. (7)

В формуле (7) вместо х подставим х² и получим разложение новой функции:

. (8)

Так как степенные ряды являются равномерно сходящимися, то их можно почленно интегрировать, и при этом интервалы сходимости остаются прежними. После интегрирования правых и левых частей формул (6)-(8) получим разложения ещё трёх функций:

, ;

, .

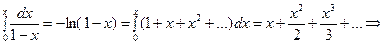
Теперь у нас есть представление в виде рядов шести функций. Но встаёт вопрос, а как разложить в степенной ряд произвольную функцию? Решение этой задачи сводится к нахождению коэффициентов а_n для конкретной функции.

Вначале функцию представим в виде степенного ряда вблизи нуля: . В этом случае легко догадаться, как найти коэффициент а₀: нужно положить х = 0. Оказалось, что . Чтобы определить, чему равен следующий коэффициент а₁, нужно продифференцировать равенство по х, а потом положить х = 0:

Продолжая дифференцировать и затем считать, что х = 0, найдём все коэффициенты а_n.

В результате получается ряд, который называется рядом Маклорена:

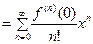В общем случае, если 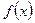имеет в некоторой окрестности т. х₀ производные до (n + 1)-го порядка включительно, то в этой окрестности она может быть представлена формулой Тейлора:

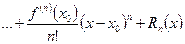где называется остатком ряда Тейлора.

Существуют различные формы остаточного члена, но наиболее употребительной является форма Лагранжа:

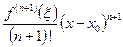=, где .

В этом виде остаток ряда напоминает (n+1)-й член формулы Тейлора, но (n+1)-я производная берётся не в т. х₀, а в некоторой промежуточной точке, лежащей между х₀ и х.

Ряд Тейлора сходится к порождающей его функции тогда и только тогда, когда в формуле Тейлора стремится к 0 при . Если в некоторой т. х остаток ряда не стремится к нулю, то ряд Тейлора может расходиться в этой точке или сходиться, но к другой функции.

Таким образом, чтобы разложить функцию в степенной ряд, нужно:

1) вычислить производные 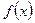в данной точке и найти коэффициенты ряда Тейлора;

2) выписать остаточный член формулы Тейлора и найти те значения х при которых стремится к 0, т.е. найти интервал, в котором данная функция разлагается в степенной ряд (является его суммой).

Пример 1.Разложить в ряд Маклорена функцию 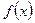= е ^х.

Решение. Вычислим значения функции и её производных при х = 0:

, .

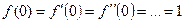Получим ряд:

Остаточный член формулы Тейлора имеет вид ==.

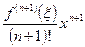При любом 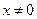дробь стремиться к 0 при , а 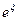является ограниченной величиной. Значит, 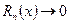при для 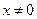, а если х = 0, то = 0.

Таким образом, ряд Маклорена для функции е^х сходится к этой функции на всей числовой оси:

. (9)

Пример 2.Разложить в ряд Маклорена функци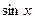и и .

Решение. Рассмотрим функцию 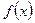=и её производные: , , , , , …. В нуле они равны , , , , , , ….

Видим, что производные нечётного порядка при х = 0 равны ±1 (знаки чередуются), а все чётные производные равны 0. Значит, ряд Маклорена будет содержать только нечётные степени х, как и следовало ожидать в силу нечётности :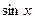

. (10)

Остаточный член формулы Тейлора функции 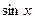будет содержать кроме дроби сомножитель , модуль которого ограничен единицей, а значит, 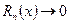при при любом х. Таким образом, ряд (10) сходится к на всей числовой оси.

Для функции : , производные при чётного порядка равны ±1 (знаки чередуются), а производные нечётного порядка равны 0. И также, как для 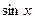остаток ряда 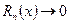при для всех х. В результате получим

Пример 3.Разложить в ряд Маклорена , где m Î R (если m – натуральное число, то получим разложение по формуле бинома Ньютона).

Решение. Вычислив производные данной функции, найдём ряд Маклорена для данной функции:

сходимость которого можно установить по признаку Даламбера. Такой ряд сходится к данной функции только на интервале (–1, 1), он называется биномиальным рядом для функции .

Приведём частные случаи биномиального ряда.

При m = –1: , что совпадает с формулой (7).

При :

. (11)

При :

Пример 4. Найти ряд Маклорена для и .

Решение. Воспользуемся формулой (11), заменив в ней х на -х²и после этого проинтегрировав правую и левую часть равенства:

, .