Область сходимости степенного ряда

План лекции

Лекция 6. Степенные ряды

Озерная (лимническая) группа континентальных отложений

Озерные отложения являются субаквальными образованиями, и те из них, которые образуются в крупных озерах, по своей характеристике стоят ближе к морским, чем к континентальным отложениям. Особенно это относится к таким обширным солоноватоводным замкнутым водоемам, как Каспийское или Аральское моря, осадки которых являются морскими. В лимническую группу не входят также осадки старичных озер речных пойм и временных озеровидных разливов, периодически возникающих по периферии крупных конусов выноса в аридных климатических обстановках. Они относятся, соответственно, к аллювию и пролювию и должны рассматриваться как их озерные фации. Отложения приледниковых озер выделяются в особую группу ледникового ряда. Такое ограничение лимнической группы отложений вносит в классификационную схему некоторую условность, т.к. все члены сложного континентального осадочного комплекса тесно взаимосвязаны.

Характер озерных осадков в значительной степени определяется климатом, который влияет на гидрологию водоемов, гидрохимию вод и массу органического вещества, образуемого водными организмами.

В пресноводных проточных озерах гумидных климатических зон накапливаются илы с железо-марганцевыми конкрециями (озерные руды), сапропели (торфянистые и водорослевые) и диатомиты.

В солоноватоводных и соленых бессточных озерах аридных зон – биохемогенные карбонатные (известковые и доломитовые) илы и самоосадочные соли (гипс, мирабилит, поваренная соль). В засушливых условиях накапливаются хемогенные осадки.

Но в одной и той же климатической зоне сосуществуют озера с разным составом осадков, зависящим от размеров и морфологии озерного водоема, площади, рельефа и геологического строения водосбора. Поэтому в разных озерах могут преобладать то песчано-алевритовые и глинистые осадки (особенно в горах), то чисто органогенные илы.

Характер напластования и присутствие остатков диатомовых водорослей, пыльцы и спор высших растений делают некоторые разновидности озерных отложений важными объектами климатостратиграфических исследований.

6.1. Область сходимости степенного ряда

6.2. Разложение функций в степенные ряды

6.3. Применение степенных рядов в приближённых вычислениях

Функциональный ряд вида

называется степенным рядом, где постоянные числа являются коэффициентами степенного ряда.

Простейшим степенным рядом будет ряд, в котором все а_n = 1: . Очевидно, что это упомянутая в п. 4.2.1 бесконечная сумма членов геометрической прогрессии (1), первый член которой равен а = 1, а знаменатель - q = х. В соответствии с формулой (2) этот ряд сходится при , и в этом случае его сумма будет функцией х:

. (5)

Теорема Абеля. Если степенной ряд сходится в т. 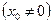, то ряд сходится абсолютно для всех х, для которых < . Если степенной ряд расходится в т. х₁ , то он расходится при всех значениях х, для которых > .

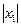Из теоремы Абеля следует, что существует некоторый интервал с центром в т. х = 0, внутри которого ряд сходится абсолютно, а вне интервала – расходится. Этот интервал называется интервалом сходимости, а положительное число R – радиусом сходимости. Если ряд расходится при всех значениях х, кроме х = 0, то R = 0; если ряд сходится при всех значениях х (на всей числовой оси), то .

Рассмотрим степенной ряд более общего вида 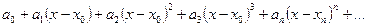, из которого подстановкой можно получить приведённый выше ряд . Если радиус сходимости нового ряда равен R, то предыдущий сходится при всех х, для которых < R. Отсюда следует: << , <<, т.е. интервал сходимости симметричен относительно т. х₀ (рис. 3). При > R ряд расходится.

Рис. 3. Интервал сходимости степенного ряда

Для нахождения области сходимости степенного ряда удобно пользоваться признаками Даламбера или радикальным Коши . Из-за того, что члены функционального ряда при различных х могут быть как положительными, так и отрицательными, в пределах поставлены модули. При этом концы интервалов исследуются отдельно, так как на концах указанные пределы равны 1, и данные признаки ответа не дают.

Пример. Найти область сходимости степенного ряда .

Решение. Данный ряд является степенным, и , . Вычислим предел:

Ряд сходится по признаку Даламбера, если < 1 Þ < 3 Þ –3 < х < 3. В этом интервале ряд сходится абсолютно, а при > 3 расходится. Концы интервала надо исследовать отдельно.

Подставив х = 3 в исходный ряд, получим

Этот ряд расходится как обобщённый гармонический со степенью < 1.

Подставив х = –3 в данный ряд, получим ряд . Ряд знакочередующийся и по признаку Лейбница сходится, так как члены ряда монотонно убывают по абсолютной величине (>), и общий член ряда стремится к нулю при ().

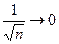Следовательно, областью сходимости данного ряда является полуоткрытый интервал .

Степенные ряды являются равномерно сходящимися. Поэтому на них распространяются свойства этих рядов. Ещё раз их перечислим.

1. Сумма степенного ряда есть функция, непрерывная в интервале сходимости ряда.

2. Степенной ряд можно почленно дифференцировать и интегрировать в интервале сходимости, и при этом полученные ряды имеют тот же интервал сходимости.