Тригонометрическая форма комплексного числа

Заданием модуля и аргумента комплексное число определяется однозначно.

Действительная и мнимая части к.ч. выражаются через его модуль и аргумент следующим образом:

, .

Модуль и аргумент к.ч. определяются из условий:

(*)

Пример. Найти модуль и аргументы комплексного числа .

В данном случае , . Система (*) имеет вид

Из алгебраической формы к.ч. всегда видно, в каком квадранте комплексной плоскости расположено к.ч. Число находится в 4-ой координатной четверти (в этой четверти косинус принимает положительные значения, а синус – отрицательные), и его значение . Таким образом, , .

Пример. Какие множества точек комплексной плоскости задаются условиями: 1) ; 2) ?

Решение

1) Условию удовлетворяют те и только те точки комплексной плоскости, которые удалены от точки на расстояние, равное единице. Такие точки лежат на окружности единичного радиуса с центром в точке .

0 1

2) К.ч. 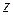, удовлетворяющие неравенствам , удалены от точки на расстояние большее или равное двум, но меньшее трех. Такие точки расположены внутри и на внутренней границе кольца, образованного двумя концентрическими окружностями с центром в точке и с радиусами и .

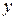
Каждое комплексное число , отличное от нуля, может быть записано в тригонометрической форме

Тригонометрическая форма записи к.ч. оказывается очень удобной при умножении, делении комплексных чисел, а также при возведении в степень и извлечении целой положительной степени к.ч.

Пусть , .

;

(формула Муавра);

;

, где .

· Модуль произведения двух комплексных чисел равен произведению модулей этих чисел, а аргумент равен сумме аргументов сомножителей:

; .

· Модуль целой положительной степени к.ч. равен такой же степени модуля к.ч., а аргумент степени равен аргументу числа, умноженному на показатель степени:

, .