Геометрическая интерпретация комплексных чисел
Известно, что между множеством упорядоченных пар действительных чисел  и множеством всех точек плоскости может быть установлено взаимно однозначное соответствие.
и множеством всех точек плоскости может быть установлено взаимно однозначное соответствие.
Представим комплексное число  как упорядоченную пару действительных чисел
как упорядоченную пару действительных чисел  . Следовательно, каждому комплексному числу
. Следовательно, каждому комплексному числу  может быть поставлена в соответствие точка плоскости
может быть поставлена в соответствие точка плоскости  , и наоборот.
, и наоборот.
Это дает возможность рассматривать комплексные числа как точки координатной плоскости, которую называют комплексной плоскостью.
Ось абсцисс называется действительной осью  (на ней расположены точки, соответствующие числам
(на ней расположены точки, соответствующие числам  ), ось ординат – мнимой осью
), ось ординат – мнимой осью  (на ней лежат точки, соответствующие мнимым числам
(на ней лежат точки, соответствующие мнимым числам  ).
).


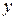


0 

Часто удобно истолковывать комплексное число  как вектор
как вектор  . Это позволяет дать простое геометрическое истолкование операциям над комплексными числами:
. Это позволяет дать простое геометрическое истолкование операциям над комплексными числами:
1) при сложении комплексных чисел их радиус-векторы складываются (по правилу параллелограмма),
2) при вычитании к.ч. их радиус-векторы вычитаются;
3) модуль разности к.ч. есть расстояние между точками комплексной плоскости, которые соответствуют этим числам;
4)  - модуль суммы комплексных чисел не превосходит суммы модулей чисел-слагаемых
- модуль суммы комплексных чисел не превосходит суммы модулей чисел-слагаемых





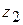


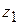
0 



Пример.Дать геометрическое истолкование сумме и разности комплексных чисел  и
и  .
.
· Модулем  комплексного числа
комплексного числа  называется длина соответствующего этому числу вектора:
называется длина соответствующего этому числу вектора:
 .
.
Комплексные числа, имеющие один и тот же модуль  , соответствуют точкам комплексной плоскости, расположенным на окружности радиуса
, соответствуют точкам комплексной плоскости, расположенным на окружности радиуса  с центром в начале координат.
с центром в начале координат.



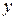



Зная модуль числа, можно однозначно задать комплексное число можно, задав направление вектора 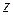 с помощью величины угла
с помощью величины угла  .
.
· Аргументом комплексного числа  называется величина угла между положительным направлением действительной оси и вектором
называется величина угла между положительным направлением действительной оси и вектором 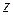 .
.
Величина угла считается положительным, если отсчет ведется против часовой стрелки, и отрицательной, если по часовой стрелке.
Аргумент к.ч., в отличие от модуля, определяется не однозначно. Например, аргументами к. ч.  являются углы
являются углы  ,
,  ,
,  и, вообще, каждый из углов
и, вообще, каждый из углов  , где
, где  - произвольное действительное число. Любые два аргумента отличаются на число, равное
- произвольное действительное число. Любые два аргумента отличаются на число, равное  .
.









Таким образом,
 , где
, где  ,
, 
· Главным значением  аргумента к.ч. называется наименьшее по модулю значение аргумента, причем
аргумента к.ч. называется наименьшее по модулю значение аргумента, причем  .
.