Равномерная сходимость
Функциональный ряд называется равномерно сходящимся на отрезке [a, b], если для всякого e > 0 можно найти такой номер N, что при n > N и любом х на отрезке [a, b] будет выполнено неравенство 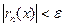 .
.
Признак равномерной сходимости Вейертрасса. Функциональный ряд сходится абсолютно и равномерно на отрезке [a, b], если существует сходящийся числовой ряд с положительными членами 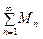 такой, что
такой, что  .
.
Ряд 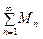 называется мажорирующим (усиливающим), или мажорантой.
называется мажорирующим (усиливающим), или мажорантой.
Пример. Ряд 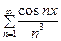 равномерно сходится для х Î R, так как мажоранта
равномерно сходится для х Î R, так как мажоранта 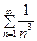 (
(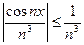 ) сходится, так как является обобщённым гармоническим рядом Дирихле с показателем степени большим единицы (см. пример п. 4.2.3.5).
) сходится, так как является обобщённым гармоническим рядом Дирихле с показателем степени большим единицы (см. пример п. 4.2.3.5).
Перечислим важные свойства равномерно сходящихся рядов.
1. Если ряд из непрерывных функций равномерно сходится в области D, то его сумма есть непрерывная функция в этой области.
2. Равномерно сходящийся ряд можно почленно интегрировать, т.е.  .
.
3. Если ряд, составленный из производных сходящегося ряда, сходится равномерно, то его можно почленно дифференцировать, т.е. 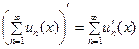 .
.
Пример. Можно ли почленно дифференцировать функциональный ряд  ?
?
Решение. Исходный ряд равномерно сходится по признаку Вейертрасса, так как мажорирующий ряд 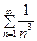 сходится. Однако ряд, составленный из производных его членов, расходится, так как не выполняется необходимое условие сходимости ряда, заключающееся в стремлении к нулю общего члена ряда при стремлении n к бесконечности:
сходится. Однако ряд, составленный из производных его членов, расходится, так как не выполняется необходимое условие сходимости ряда, заключающееся в стремлении к нулю общего члена ряда при стремлении n к бесконечности:
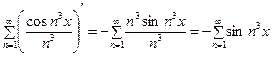 .
.
Вывод: исходный ряд почленно дифференцировать нельзя.