Пример 1. Исследовать совместность системы уравнений

Решение.A = . Найдем r(А). Так как матрица А имеет порядок 3х4, то наивысший порядок миноров равен 3. При этом все миноры третьего порядка равны нулю (проверить самостоятельно). Значит, r(А) < 3. Возьмем главный базисный минор = -5-4 = -9 ≠ 0. Следовательно r(А) =2.

Рассмотрим матрицу С = .

Минор третьего порядка ≠ 0. Значит, r(C) = 3.

Так как r(А) ≠ r(C) , то система несовместна.

Пример 2. Определить совместность системы уравнений

Решить эту систему, если она окажется совместной.

 

Решение.

A = , C = 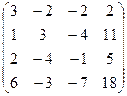. Oчевидно, что r(А) ≤ 3, r(C) ≤ 4. Так как detC = 0, то r(C) < 4. Рассмотрим минор третьего порядка, расположенный в левом верхнем углу матрицы А и С: = -23 ≠ 0. Значит, r(А) = r(C) = 3.

Число неизвестных в системе n=3. Значит, система имеет единственное решение. При этом четвертое уравнение представляет сумму первых трех и его можно не принимать во внимание.

По формулам Крамера получаем x₁ = -98/23, x₂ = -47/23, x₃ = -123/23.

 

2.4. Mатричный метод. Mетод Гаусса

 

Систему n линейных уравнений с n неизвестными можно решать матричным методом по формуле X = A^-1B (при Δ ≠ 0 ), которая получается из (2) умножением обоих частей на А^-1.

Пример 1. Решить систему уравнений

матричным методом ( в параграфе 2.2 эта система была решена по формулам Крамера)

Решение. Δ = 10 ≠ 0 А = - невырожденная матрица.

= (убедитесь в этом самостоятельно, произведя необходимые вычисления).

A^-1 = (1/Δ)х= .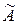

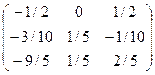Х = A^-1В = 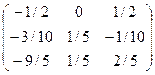х= .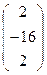

Ответ: .

С практической точки зрения матричный метод и формулы Крамера связаны с большим объемом вычислений, поэтому предпочтение отдается методу Гаусса, который заключается в последовательном исключении неизвестных. Для этого систему уравнений приводят к эквивалентной ей системе с треугольной расширенной матрицей (все элементы ниже главной диагонали равны нулю). Эти действия называют прямым ходом. Из полученной треугольной системы переменные находят с помощью последовательных подстановок (обратный ход).

Пример 2. Методом Гаусса решить систему

(Выше эта система была решена по формуле Крамера и матричным методом).

Решение.

Прямой ход. Запишем расширенную матрицу и с помощью элементарных преобразований приведем ее к треугольному виду:

~ ~ ~ ~ .

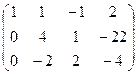Получим систему

Обратный ход. Из последнего уравнения находим х₃ = -6 и подставим это значение во второе уравнение:

х₂ = - 11/2 - 1/4 х₃ = - 11/2 – 1/4(-6) = - 11/2 + 3/2 = -8/2 = -4.

Подставляя далее х₂ = -4, х₃ = -6 в первое уравнение системы, получим:

х₁ = 2 - х₂ + х₃ = 2+4-6 = 0.

Ответ: .

 

2.5. Общее решение системы линейных уравнений

 

Пусть дана система линейных уравнений = b_i(i =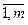). Пусть r(A) = r(C) = r, т.е. система совместна. Любой минор порядка r, отличный от нуля, является базисным минором. Не ограничивая общности, будем считать, что базисный минор располагается в первых r (1 ≤ r ≤ min(m,n)) строках и столбцах матрицы А. Отбросив последние m-r уравнений системы, запишем укороченную систему:

которая эквивалентна исходной. Назовем неизвестные х₁,….х_r базисными, а х_r+1,…, х_r свободными и перенесем слагаемые, содержащие свободные неизвестные, в правую часть уравнений укороченной системы. Получаем систему относительно базисных неизвестных:

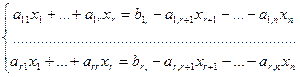
koтоторая для каждого набора значений свободных неизвестных х_r+1 = С₁,…, х_n = С_n-r имеет единственное рeшение х₁( С₁,…, С_n-r),…, х_r(С₁,…, С_n-r), находимое по правилу Крамера.

Соответствующее решение укороченной, а следовательно, и исходной системы имеет вид:

Х(С₁,…, С_n-r) = - общее решение системы.

Если в общем решении свободным неизвестным придать какие-нибудь числовые значения, то получим решение линейной системы, называемое частным.

Пример. Установить совместность и найти общее решение системы

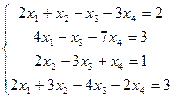
Решение. А = , С = .

Так как r(A) = r(C) = 2 (убедитесь в этом самостоятельно), то исходная система совместна и имеет бесчисленное множество решений (так как r < 4).

Выберем в качестве базисного минор . Тогда неизвестные х₁ и х₂ - базисные; х₃ и х₄ - свободные, а укороченная система имеет вид

 

Полагая х₃ = С₁, х₄ = С₂ и решая укороченную систему относительно базисных неизвестных, получаем:

х₁ = 3/4- 1/4 С₁ + 7/4 С₂,

х₂ = 1/2+ 3/2 С₁ – 1/2 С₂.

Следовательно, общее решение исходной системы имеет вид:

Х(С₁;С₂) =

 

2.6. Системы однородных уравнений

 

Система однородных уравнений = 0 (i =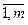) всегда является совместной, так как r(A) = r(C).

Одним из решений системы однородных уравнений является тривиальное решение х₁ = х₂ = … = х_n = 0.

Для однородной системы важно установить, имеет ли она ненулевые решения. Из теоремы Кронекера – Капелли следует, что система однородных уравнений имеет ненулевое (нетривиальное) решение тогда и только тогда, когда r(A) < n, где n – число неизвестных.

Пример 1. Определить, имеет ли система однородных уравнений

ненулевое решение. Найти это решение, если оно имеется.

Решение. detA = = 0, значит, r(A) < 3.

Минор = 6 ≠ 0 r(А) = 2. Значит, рассматриваемая система имеет ненулевые решения. Найдем их. Запишем второе и третье уравнения системы в виде х₂ = 3 х₁, х₃ = - х₁ - бесчисленное множество решений.