Определение. Уравнения

Задача Коши.

Дифференциальные уравнения высших порядков. Теорема о существовании и единственности решения.

ЛЕКЦИЯ 19

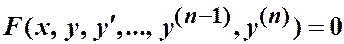
19.5.1. Теорема о существовании и единственности решения д. у. 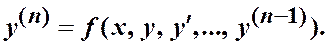(1)

Теорема. Если 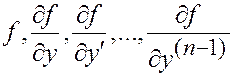непрерывны в области W Í Rⁿ⁺¹, то " т. $ единственное решение y(x) уравнения на некотором интервале оси Ox, содержащем x₀, такое, что

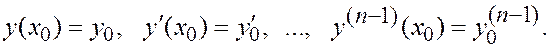(2)

 

19.5.2. Задача Коши для д. у. n-го порядка. Общее и частное решения, общий и частный интегралы. Особые решения.

Определение. Задача Коши: найти решение д.у.(1), удовлетворяющее начальным условиям (2).

 

В условиях теоремы о $ и единств. решения задача Коши " точки имеет единственное решение (задача Коши поставлена корректно).

Пример. .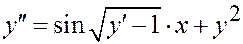

 

– не корректно (по области определения);

 

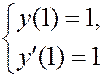– не корректно, т.к. не непрерывна;

 

– задача поставлена корректно.

Определение.Если в области W Í Rⁿ⁺¹

" т. задача Коши имеет единственное решение, то каждое из решений y(x) называется частным решением уравненияв W.

Если получена формула

y = φ(x, C₁, C₂, …, C_n )(3)

такая, что

 

а) " C₁, C₂, …, C_n из некоторого E Í Rⁿ функция

y = φ(x, C₁, C₂, …, C_n) есть частное решение в W

 

б) каждое частное решение в W может быть получено по этой формуле выбором единственных C₁, C₂, …, C_n,

то формула (3) называется общим решением д.у. в W.

 

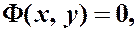
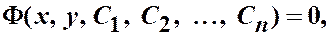
определяющие частное и общее решения в неявном виде

(т.е. имеющие те же решения, что и д. у.),

называют частным интеграломи общим интегралом д.у.

 

Определение.Решение д.у. называется особым, если в каждой точке его нарушается единственность решения задачи Коши.