План лекции
Лекция 1. Элементы теории вероятностей
Математическая статистика
Теория вероятностей
Курс лекций по высшей математике
для студентов инженерно-технических
специальностей
1.1. Случайные события и их вероятности
1.2. Основные формулы теории вероятностей
1.3. Схема Бернулли
1.1. СЛУЧАЙНЫЕ СОБЫТИЯ И ИХ ВЕРОЯТНОСТИ
С глубокой древности люди в своей деятельности сталкивались с непредсказуемыми результатами своих действий и вероятностным характером явлений природы. Так первобытный вождь понимал, что шансы поразить копьем мамонта у десяти охотников гораздо больше, чем у одного. По мере накопления научных знаний человек, анализируя события, стал классифицировать их как достоверные, возможные и невозможные. Было замечено, что случайностями часто управляют объективные законы. Например, в начале ХХ века английский математик Пирсон провел эксперимент: 24 000 раз подбросил монету. Герб при этом выпал 12 012 раз. В середине ХХ столетия американские экспериментаторы повторили этот опыт, и при 10 000 подбрасываний герб выпал 4 979 раз. Результат опыта – случайное событие, но при многократных подбрасываниях монеты число выпавших гербов приблизительно равно половине числа испытаний, а это уже объективная закономерность. Или, была подмечена закономерность в исходах многих опытов различной природы (результаты измерений физических величин, скорости молекул в газе, рост и вес новорожденных и т.д.): значения случайных величин подчиняются закону нормального распределения.
Впервые последовательно основы раздела математики, который позже станет называться теорией вероятностей, были изложены французским математиком Лапласом (1749-1827) в книге «Аналитическая теория вероятностей». Обозначим основные понятия этой науки.
Будем называть опытом воспроизведение некоторой совокупности условий, позволяющих наблюдать интересующее нас явление.
Достоверным называется событие W, которое обязательно произойдет в результате опыта, если будет осуществлена определенная совокупность условий.
Невозможным называется событие Æ, которое заведомо не произойдет, если будет осуществлена определенная совокупность условий.
Событие (явление), которое в результате данного опыта может произойти, а может и не произойти, называют случайным. Обозначают такие события строчными латинскими буквами: А, В, С, …. Случайные события могут подчиняться простым или более сложным закономерностям.
Случайные события называются равновозможными, если оснований считать, что одно из них может реализоваться в опытах чаще, чем другие, у нас нет. Например, при подбрасывании монеты выпадения герба и решки равновозможны. Или ещё пример: бросается кость (кость – это кубик, на гранях которого написаны цифры 1, 2, 3, 4, 5, 6). Если кубик однородный (сделан из материала с постоянной плотностью), то выпадение любой из граней равновозможно.
События называются несовместными, если они не могут произойти одновременно в результате некоторого опыта.
Событие 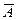 противоположно событию А, если оно несовместно с А и вместе с ним образует достоверное событие: А +
противоположно событию А, если оно несовместно с А и вместе с ним образует достоверное событие: А +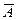 = W.
= W.
События называются независимыми, если наступление одного из них не оказывает никакого влияния на появление другого (например, независимы очки, выпавшие у двух человек на игральных костях).
З а м е ч а н и е. Если события А и В независимы, то можно доказать, что пары событий: 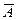 , В;
, В; 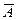 ,
, 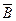 и
и 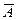 ,
, 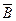 также являются независимыми.
также являются независимыми.
П р и м е р. Бросается кость. Введём обозначения событий: А1 – выпало одно очко, …, А6 – выпало шесть очков, В – выпало более 10 очков, С – выпало не менее одного очка.
В рассматриваемом примере событие В невозможное, т.е. В = Æ, ибо больше 6 очков в результате опыта не может выпасть. Событие С – достоверное, т.е. С = W, т.к. меньше одного очка выпасть не может. Любая пара событий (например, А1 и А3 или А2 и А6) является несовместной, поскольку в результате бросания кости реализуется только одно из случайных событий А1, А2, …, А6. Событие “не выпало ни одного очка” - невозможное: 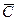 = Æ.
= Æ.
Под суммой случайных событий А и В понимается случайное событие С (пишут С = А + В), состоящее в том, что происходит хотя бы одно из событий А или В. Т.е. событие С состоит в том, что произошло или событие А, или В, или А и В одновременно.
Пусть событие А происходит всегда, когда случается и событие В. Тогда можно ввести понятие разности событий А - В, которая состоит в появлении события А и не появлении события В.
Под произведением случайных событий А и В понимается случайное событие С (пишут С = А × В), состоящее в том, что произошло и событие А, и событие В.
З а м е ч а н и е. Если события А, В, С интерпретировать как некоторые множества, то С = А + В означает, что С = АÈВ, а С = А × В – это С = АÇВ.
Приведём очевидные соотношения между событиями: А + W = W; А × W = А; А + Æ = А; А × Æ = Æ.
П р и м е р ы.
1. Производится выстрел в мишень. Событие А – мишень поражена, В – промах. Тогда сумма А + В = W, т.к. результатом выстрела в мишень будет или попадание, или промах. Произведение А × В = Æ, т.к. одновременно поразить мишень и промахнуться невозможно.
2. Бросается кость. Тогда сумма А1 + А2 + А3 + А4 +А5 + А6 = W - достоверное событие, т.к. какое-то из шести событий обязательно происходит. Сумма, например, А1 + А2 + А3 +А4 представляет событие, которое состоит в том, что при выбрасывании кости выпало не более четырех очков. Произведение Аi × Ai = Ai, i = 1, …, 6. А вот произведение Аi × Aj = Æ, если i ¹ j, i, j = 1, 2,…, 6, т.к. любые два события Аi и Аj несовместны.
Основным же понятием в теории вероятностей является вероятность события А, которая Лапласом была определена как
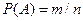 , (1.1)
, (1.1)
где n – число равновозможных исходов опытов; m – число исходов, когда произошло событие А, или, как говорят, число исходов, благоприятствующих появлению случайного события А.
Вероятность события А, определённая по формуле (1.1), называется классической.
П р и м е р. Бросается кость. Какова вероятность того, что выпадет меньше 5 очков?
Р е ш е н и е. В результате опыта (опыт – бросание кости) происходит одно из шести равновозможных событий: А1 – выпало одно очко, …, А6 – выпало шесть очков. Событию А (выпало меньше пяти очков) благоприятствуют события А1, А2, А3, А4. Итак, n = 6 и m = 4, поэтому искомая вероятность равна 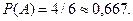
Классическая вероятность базируется на понятии «равновозможности» случайных событий, что ассоциируется с человеческим «кажется», но объективная реальность необязательно совпадает с субъективным «кажется». Возникла потребность «перепроверять» вероятности, вычисленные по формуле (1). Эта «перепроверка» привела к следующей статистической оценке возможности появления события А: пусть проведено n опытов, в которых событие А реализовалось m раз; тогда частотой события А называют величину 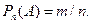 В этом случае за вероятность события А принимается постоянная величина, около которой группируются наблюдаемые значения частот. Другими словами,
В этом случае за вероятность события А принимается постоянная величина, около которой группируются наблюдаемые значения частот. Другими словами, 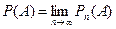 , если, конечно, предел существует. Такую вероятность называют статистической.
, если, конечно, предел существует. Такую вероятность называют статистической.
Наконец, существует аксиоматическая теории вероятностей, построение которой связано с именем советского математика А.Н. Колмогорова (1903–1987). Для случая, когда число случайных событий является конечным, эти аксиомы были сформулированы так.
Первая аксиома: любому случайному событию А ставится в соответствии число Р(А), называемое вероятностью события А, причем считается, что 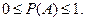
Вторая аксиома: если события А и В несовместны, то Р(А + В) = Р(А) + Р(В).
Третья аксиома: 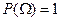 .
.
1.2. ОСНОВНЫЕ ФОРМУЛЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ
Воспользовавшись приведёнными выше аксиомами легко получить формулы для вероятностей невозможного и противоположного событий, а также разности событий.
Вероятность невозможного события равна нулю. Действительно, т.к. события W и Æ несовместны, то W + Æ = W. Отсюда Р(W) = Р(W + Æ) = Р(W) + Р(Æ) = = 1 + Р(Æ) = 1. Из этого следует, что P(Æ) = 0. Заметим однако, что из равенства Р(А) = 0 не следует, что событие А – невозможное (см. раздел 2.4).
Вероятности события А и противоположного ему события  связаны соотношением:
связаны соотношением: 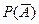 = 1 – Р(А). Действительно, т.к. события А и
= 1 – Р(А). Действительно, т.к. события А и 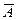 несовместны, а их сумма – достоверное событие ( А +
несовместны, а их сумма – достоверное событие ( А +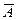 = W ), то
= W ), то  Р(А) + Р(
Р(А) + Р(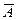 ) = Р(W) = = 1, откуда и следует это утверждение.
) = Р(W) = = 1, откуда и следует это утверждение.
Вероятность разности событий равна: . Действительно, события (А – В) и В несовместны, причем (А – В) + В = А. Поэтому Р(А) = = Р[(А - В) + В] = Р(А - В) + Р(В), и мы получаем приведённое выше равенство.
. Действительно, события (А – В) и В несовместны, причем (А – В) + В = А. Поэтому Р(А) = = Р[(А - В) + В] = Р(А - В) + Р(В), и мы получаем приведённое выше равенство.
З а д а ч а. Бросается игральная кость. Пусть событие А – выпадение чётного числа очков, а В – выпадение “4”. Найти вероятности событий: 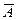 (выпадение нечётного числа очков),
(выпадение нечётного числа очков), 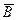 (выпадение не “4”) и А - В (выпадение “2” или “6”).
(выпадение не “4”) и А - В (выпадение “2” или “6”).
Р е ш е н и е . Очевидно, что Р(А) = 1/2, а Р(В) = 1/6. Поэтому 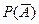 = 1/2, Р(
= 1/2, Р(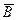 ) = 5/6, Р(А¾В) = 1/2 ¾ 1/6 = 1/3.
) = 5/6, Р(А¾В) = 1/2 ¾ 1/6 = 1/3.
Вероятность суммы случайных событий
Пусть А и В – произвольные случайные события. Если вдуматься в определения суммы, разности и произведения случайных событий, то можно понять, что два события А + В и ( А – А × В ) + В - по сути одно и то же событие. Но события (А – А × В) и В несовместны. Тогда Р(А + В) = Р[(А – А × В) + В] = Р(А – А × В) + Р(В) = Р(А) – Р(А × В) + Р(В). В результате получаем теорему сложения вероятностей:
Р(А + В) = Р(А) + Р(В) – Р(А × В).
П р и м е р. Вероятность вытащить из колоды, содержащей 36 карт, или даму (А), или пиковую масть (В) равна Р(А+В) = Р(А) + Р(В) – Р(А×В) = 4/36 + 1/4 – – 1/ 36 = 1/3. Здесь учтено, что событие А×В – это вытаскивание пиковой дамы.
З а д а ч а. В соревновании участвуют два спортсмена. Вероятность того, что первый улучшит свой личный рекорд, равна 0,05, а а для второго эта вероятность равна 0,3. Найти: 1) вероятность того, что ни один из спортсменов не улучшит своё личное достижение; 2) только один улучшит свой рекорд. Результаты выступлений спортсменов считаются независимыми.
Р е ш е н и е. Введем события: А1 – первый спортсмен улучшил свой рекорд, А2 – второй улучшил. Тогда событие 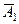 –первый спортсмен не улучшил рекорд,
–первый спортсмен не улучшил рекорд, 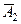 – второй не улучшил.
– второй не улучшил.
1. Надо найти вероятность события 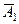 ×
×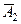 , состоящего в том, что никто из спортсменов не улучшил свой рекорд. Поскольку эти события независимы, то вероятность произведения двух событий равна произведению их вероятностей:
, состоящего в том, что никто из спортсменов не улучшил свой рекорд. Поскольку эти события независимы, то вероятность произведения двух событий равна произведению их вероятностей: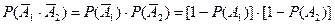 = 0,95×0,7 = 0,665.
= 0,95×0,7 = 0,665.
2. Событие А1 × 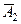 обозначает, что первый спортсмен улучшил свой рекорд, а второй - не улучшил, событие же
обозначает, что первый спортсмен улучшил свой рекорд, а второй - не улучшил, событие же  × А2 – с точностью до наоборот, причём эти события несовместны. Сумма событий А1 ×
× А2 – с точностью до наоборот, причём эти события несовместны. Сумма событий А1 × 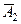 +
+  × А2 означает, что только один из спортсменов улучшил свое личное достижение. С учётом независимости результатов выступлений спортсменов вероятность этой суммы равна Р(А1 ×
× А2 означает, что только один из спортсменов улучшил свое личное достижение. С учётом независимости результатов выступлений спортсменов вероятность этой суммы равна Р(А1 × 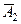 +
+  × А2) = Р(А1 ×
× А2) = Р(А1 × 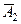 ) + Р(
) + Р( × А2) – Р[(А1 ×
× А2) – Р[(А1 × 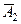 ) × (
) × ( × А2)] = P(А1) × P (
× А2)] = P(А1) × P (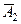 ) + P(
) + P(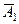 ) × P(А2) = 0,05 × 0,7 + 0,95 × 0,3 = 0,32.
) × P(А2) = 0,05 × 0,7 + 0,95 × 0,3 = 0,32.
Условные вероятности
Для произвольных событий А и В вероятность их произведения считается равной 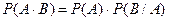 , где Р(В/А) называется условной вероятностью, т.е. вероятностью события В при условии, что событие А уже произошло. Можно также записать Р(А × В) = Р(В) × Р(А/В), где Р(А/В) - тоже условная вероятность, но уже события А при условии, что произошло событие В.
, где Р(В/А) называется условной вероятностью, т.е. вероятностью события В при условии, что событие А уже произошло. Можно также записать Р(А × В) = Р(В) × Р(А/В), где Р(А/В) - тоже условная вероятность, но уже события А при условии, что произошло событие В.
Вероятности Р(А) и Р(В) можно назвать априорными, что означает “до опыта” или “до того, как”. А вероятности Р(А/В) и Р(В/А) – апостериорными, т.е. “после опыта” или “после того, как”.
Вероятность произведения двух несовместных событий, как следует из их определения, равна нулю.
Если А и В независимые события, то вероятность произведения таких событий определяется по формуле: Р(А × В) = Р(А) × Р(В) (так даже определяют независимость случайных событий). Если сравнить эту формулу с общей: Р(А × В) = Р(В) × Р(А/В), то приходим к заключению, что Р(А) = Р(А/В).
При 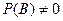 из равенства
из равенства 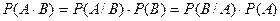 следует формула Бейеса, которая позволяет по известным априорным вероятностям событий А и В и одной из апостериорных вероятностей, вычислить другую апостериорную вероятность:
следует формула Бейеса, которая позволяет по известным априорным вероятностям событий А и В и одной из апостериорных вероятностей, вычислить другую апостериорную вероятность:
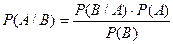 .
.
Легко показать, что: 1) P(W/A) = 1, 2) P(A/A) = 1, 3) если А1 и А2 независимые события, то Р[(А1+А2)/B] = Р(А1/B) + Р(А2/B).
Формула полной вероятности
Пусть события А1, А2, …, Аn попарно несовместны, т.е. Ai ×Aj = Æ, где i ¹ j; i = 1, 2, …, n; j = 1, 2, …, n. Пусть также А1 + А2 + …+ Аn = W, т.е. одно из этих событий обязательно происходит (про такие события говорят, что они образуют полную группу событий). Тогда для любого события В, связанного с событиями Ai, можно написать следующие равенства: В = В × W = В × (А1 + А2 + …+ Аn) = B × A1 + B × A2 + … + B × An. В силу очевидной несовместности любой пары событий (Ai × × B и Aj × B, i ¹ j) получаем: P(B) = P (B × A1 + B × A2 + …+ B × An) = P(A1× B) + P(A2× × B) + … + P(An × B) = P(A1) × P(B/A1) + P(A2) × P(B/A2) + … + P(An) × P(B/An). Это соотношение называется формулой полной вероятности:
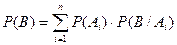 ,
,
а события Ai – гипотезами.
Теорема Бейеса
Комбинация формул Бейеса и полной вероятности позволяет получить формулу, являющуюся содержанием теоремы Бейеса.
Пусть события А1,…, Аn образуют полную группу, т.е. А1 + А2 + …+ Аn = W; Ai × Aj = Æ; i ¹ j. Тогда для любого события В с ненулевой вероятностью справедлива формула:
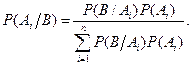
Д о к а з а т е л ь с т в о. В условиях данной теоремы справедлива формула Бейеса
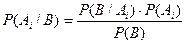
и формула полной вероятности
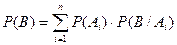 .
.
Поэтому получаем
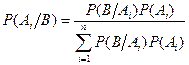 .
.
З а д а ч а № 1. Первый стрелок поражает мишень с вероятностью 0,8, а второй с вероятностью 0,3. Право на выстрел разыгрывается с помощью жребия: бросается монета, если выпадает герб, то стреляет первый стрелок, в противном случае – второй. Какова вероятность поражения мишени при одном выстреле?
Р е ш е н и е . Обозначим события: А1 - стреляет первый стрелок; А2 - стреляет второй; В - мишень поражена. По условию задачи Р(В/А1) = 0,8; Р(В/А2) = 0,3;
Событие А1 означает, что выпал герб, а А2 – выпала решка. Так как события А1 и А2 являются равновозможными, то Р(А1) = Р(А2). Кроме того, сумма несовместных событий – достоверное событие: А1 + А2 = W. Поэтому Р(А1 + А2) = Р(W) = 1 = Р(А1) + Р(А2) = 2Р(А1), т.е. Р(А1) = Р(А2) = 0,5.
Формула полной вероятности позволяет вычислить искомую вероятность поражения мишени при одном выстреле: Р(В) = Р(В/А1) × Р(А2) + Р(В/А2) × Р(А2) = = 0,8 × 0,5 + 0,3 × 0,5 = 0,55.
З а д а ч а № 2. Пусть в условиях предыдущего примера сторонний наблюдатель, услышав выстрел и осмотрев мишень в бинокль, убедился, что она не поражена. Какова вероятность того, что: 1) стрелял первый стрелок, 2) стрелял второй стрелок?
Р е ш е н и е . В задаче требуется найти Р(А1/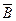 ) и Р(А2/
) и Р(А2/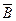 ).
).
Имеем, Р[(В+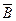 )/А1] = Р(В/А1) + Р(
)/А1] = Р(В/А1) + Р(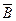 /А1) = Р(W/А1) = 1, т.е. Р(
/А1) = Р(W/А1) = 1, т.е. Р(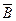 /А1) = 1 – Р(В/А1) = 1 – 0,8 = 0,2; Р(
/А1) = 1 – Р(В/А1) = 1 – 0,8 = 0,2; Р(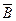 ) = 1 – Р(В) = 1 – 0,55 = 0,45.
) = 1 – Р(В) = 1 – 0,55 = 0,45.
Аналогично вычисляем Р(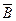 /А2) = 1 – Р(В/А2) = 1 – 0,3 = 0,7.
/А2) = 1 – Р(В/А2) = 1 – 0,3 = 0,7.
Теперь находим интересующие нас вероятности:
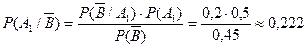 ,
,
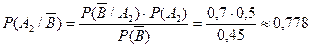 .
.
1.3. СХЕМА БЕРНУЛЛИ
Формула Бернулли
Многие задачи, имеющие разную природу (физическую, военную, медицинскую, социологическую и др.), сводятся к так называемой схеме испытаний Бернулли, суть которой состоит в следующем.
Проводится n одинаковых опытов с независимыми исходами. В результате каждого опыта событие А происходит с вероятностью р = Р(А). Вероятность противоположного события равна q = 1 - p. Какова вероятность того, что при этом событие А произойдёт ровно k раз (0£ k £ n)?
Оказывается, искомую вероятность Рn(k) можно вычислить по формуле Бернулли:
Pn(k) = Cnk pk qn-k , (1.2)
где 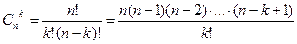 - это число сочетаний из n по k; величина n! вычисляется по формуле n! = 1×2×3×…×n, если n ³ 2; 0! = 1! = 1 и читается как “n – факториал”.
- это число сочетаний из n по k; величина n! вычисляется по формуле n! = 1×2×3×…×n, если n ³ 2; 0! = 1! = 1 и читается как “n – факториал”.
З а д а ч а №1 . Монета подбрасывается 10 раз. Какова вероятность того, что герб выпадет только 2 раза?
Р е ш е н и е . Это задача на схему Бернулли с вероятностью события (выпадение герба) р = 0,5. Число испытаний n = 10, а число благоприятных исходов k = = 2.
Вычислим искомую вероятность по формуле Бернулли:
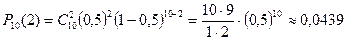 .
.
З а д а ч а №2 (задача шевалье де Мере). Какова вероятность того, что при 24 – кратном бросании двух игральных костей хотя бы один раз появятся две шестерки?
Р е ш е н и е . Пусть событие А состоит в том, что при бросании двух игральных костей две шестерки не появились. Тогда противоположное событие 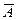 - это выпадение сразу двух шестёрок.
- это выпадение сразу двух шестёрок.
При бросании одной кости вероятность выпадения шестерки равна 1/6 (выпадение каждой цифры от 1 до 6 равновозможно). Естественно считать исходы каждого бросания кости независимыми, следовательно, вероятность того, что при выбросе двух костей появятся две шестерки Р(Ā) = 1/6 .1/6=1/36. Поэтому Р(А) = 1 – Р(Ā) = 1 – 1/36 = 35/36.
Теперь все сводится к схеме испытаний Бернулли: проводится n = 24 опыта по бросанию двух костей с независимыми исходами. Вероятность реализации события А (не выпало двух шестерок) в каждом опыте равна р = Р(А) = 35/36. Поэтому вероятность того, что в 24 опытах событие А произойдёт 24 раза равна 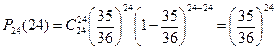 . Это событие (не будет одновременного выпадения двух шестерок при подбрасывании двух костей 24 раза) является противоположным событию: две шестёрки выпали хотя бы один раз. Поэтому искомая вероятность равна
. Это событие (не будет одновременного выпадения двух шестерок при подбрасывании двух костей 24 раза) является противоположным событию: две шестёрки выпали хотя бы один раз. Поэтому искомая вероятность равна 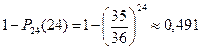 .
.
Предельные теоремы схемы Бернулли
Вычисление вероятностей по формуле (1.2) становится затруднительным при больших значениях n. Для этих случаев были выведены формулы для приближённого вычисления Pn(k).
Формула Муавра – Лапласа:
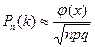 ,
,
где 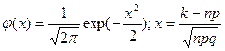 . Таблицу значений функции
. Таблицу значений функции  можно найти в любом учебнике по теории вероятностей. Её значение легко вычисляется и на “научном” (scientific) калькуляторе. Заметим, что эта функция чётная.
можно найти в любом учебнике по теории вероятностей. Её значение легко вычисляется и на “научном” (scientific) калькуляторе. Заметим, что эта функция чётная.
Формула Пуассона:
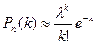 ,
,
где l = np.
При р << 1 и n >> 1 эта формула дает лучшую точность вычислений вероятности Pn(k), чем формула Муавра – Лапласа. Однако надо иметь в виду, что она применяется, если nр < 10.
З а д а ч а . Какова вероятность того, что среди 1000 случайно выбранных женщин десять родились 8 марта?
Р е ш е н и е . Полагаем, что рождение женщины в любой из 365 дней года равновозможно. Поэтому р = Р(А) = 1/365, где событие А - это рождение женщины в Международный женский день. По условию задачи n = 1000, а k = 10. По формуле Бернулли искомая вероятность равна 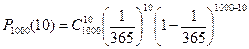 . Вычисления по этой формуле трудновыполнимы, поэтому воспользуемся формулой Пуассона, так как n – велико, р – мало, а l = np = 1000/365 » 2,74 < 10. В результате получаем значение интересующей нас вероятности
. Вычисления по этой формуле трудновыполнимы, поэтому воспользуемся формулой Пуассона, так как n – велико, р – мало, а l = np = 1000/365 » 2,74 < 10. В результате получаем значение интересующей нас вероятности
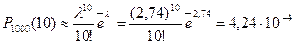 .
.
Иногда задача сводится к вычислению суммы вероятностей Рn(k) + Pn(k+1) + … + Pn(m), где k < m £ n. При больших значениях n и k вычисление таких сумм весьма трудоемко. В этом случае для приближенного вычисления суммы вероятностей используют интегральную формулу Лапласа
Pn(k, m) » Ф(xm) – Ф(xk),
где 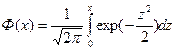 - функция Лапласа;
- функция Лапласа; 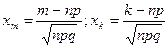 .
.
Получить выражение функции Лапласа через элементарные функции невозможно. Поэтому ввиду важности этой функции составлена таблица (см. Приложение) её значений в зависимости от х, которую можно найти в любом учебнике по теории вероятностей. Полезно иметь в виду, что Ф(x) » 0,5, если х ³ 5.
Покажем, что функция 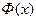 нечётная. В интеграле
нечётная. В интеграле 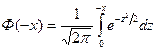 сделаем замену переменной
сделаем замену переменной 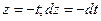 . Тогда
. Тогда 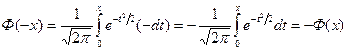 , что и требовалось доказать.
, что и требовалось доказать.
Нечётность функции Лапласа позволяет найти её значения для отрицательных значений аргумента. Например, надо узнать, чему равна функция 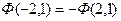 . По таблице значений функции Лапласа находим:
. По таблице значений функции Лапласа находим: 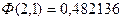 . Поэтому
. Поэтому 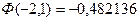 .
.
З а д а ч а №1 . Имеется 100 семян, всхожесть которых составляет 40%. Какова вероятность того, что взойдет не менее половины?
Р е ш е н и е . Это задача на схему Бернулли. Вероятность того, что посаженное семя взойдет равна р = 0,4; число опытов, заключающихся в посадке семян, равно n = 100, k = 50, m = 100.
Введем события: А1 – взошло одно семя из ста посаженных; А2 – взошло два, …, А100 – взошли все 100 семян. Надо найти Р(А50 + А51 + … + А100) = Р(А50) + Р(А51) + … + Р(А100). Каждая из этих вероятностей вычисляется по формуле Р(Аk) = Р100(k) = 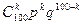 . А вероятность того, что взойдет не менее половины семян равна
. А вероятность того, что взойдет не менее половины семян равна  . Для приближенного вычисления воспользуемся интегральной (суммирующей) формулой Лапласа
. Для приближенного вычисления воспользуемся интегральной (суммирующей) формулой Лапласа 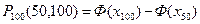 . Значения аргументов функции Лапласа равны:
. Значения аргументов функции Лапласа равны:

Воспользовавшись таблицей значений функции Ф(x), находим, что вероятность всхожести не менее половины из 100 семян равна 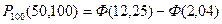 = 0,5 – 0,479 = 0,021.
= 0,5 – 0,479 = 0,021.
З а д а ч а №2 . В некотором городе в год рождается 2000 детей. Вероятность рождения мальчика равна 0,51. Какова вероятность того, что от 55% до 60% новорожденных будут мальчики?
Р е ш е н и е . В данной задаче число испытаний n = 2000, k = 0,55 × 2000 = 1100; m = 0,6 ×2000 = = 1200. Вероятность события р = 0,51, вероятность противоположного события q = 0,49.
Введем события: А0 – за год не родился ни один мальчик; А1 –родился 1 мальчик, … , А2000 – все 2000 младенцев - мальчики. Требуется найти сумму Р(А1100 ) + Р(А1101 ) + … + Р(А1200) = Р2000(1100, 1200). Вычисляем аргументы функции Лапласа: 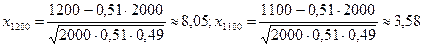 . Наконец, оцениваем искомую вероятность: Р2000(1100, 1200) = Ф(8,05) – Ф(3,58) = = 0,5 – 0,4998 = 0,0002.
. Наконец, оцениваем искомую вероятность: Р2000(1100, 1200) = Ф(8,05) – Ф(3,58) = = 0,5 – 0,4998 = 0,0002.
Из всего вышеизложенного можно сделать заключение: теория вероятностей – математическая наука, позволяющая по известным вероятностям одних случайных событий находить вероятности других случайных событий, связанных каким-либо образом с первыми.