Вычисление пределов с использованием рядов

Лекция № 4

Ряд Тейлора, Маклорена. Основные разложения.

Рассмотрим степенной ряд (2) и пусть в интервале сходимости ряда сумма его равна некоторой функции 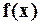т.е. :

(1)

Так как степенной ряд можно почленно дифференцировать во всём интервале сходимости (причём он также будет сходящимся в этом же интервале сходимости и сумма его равна производной от суммы исходного ряда), то продифференцируем его:

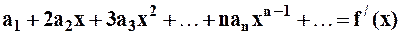, где 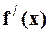– есть сумма ряда.

Дифференцируем исходный ряд “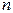” раз (причём на каждом этапе вновь будем иметь степенной ряд), в результате получим:

............................................................................................................

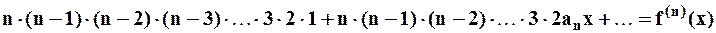
Если будем вычислять значения полученных рядов в 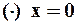, получим:

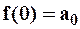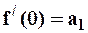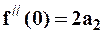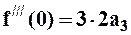, , , и т. д.

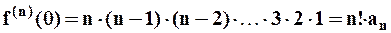и т.д.

Итак, зная, что бесконечно дифференцируемая функция является суммой степенного ряда (2), то коэффициенты этого ряда можно определить с помощью следующих формул Маклорена:

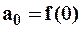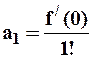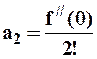, , , , и т.д.

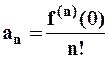, ... и т.д.

И в результате получим ряд Маклорена:

 

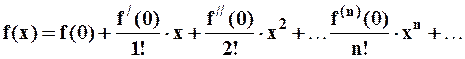
Аналогично получаются формулы Тейлора:

, , , , ..., , ...

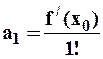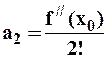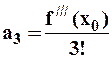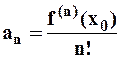При этом ряд будет иметь следующий вид:

Замечание: Не всякая функция может быть представлена в виде суммы некоторого степенного ряда. Может оказаться:

* либо сумма полученного ряда не совпадает с исходной функцией;

* либо полученный ряд не имеет конечной суммы.

Определим условия разложимости функции в ряд Тейлора (Маклорена).

Рассмотрим ряд:

(1)

Обозначим через – “”–ную частичную сумму данного ряда (1), тогда можно записать: , где – есть “” – ный остаток ряда.

Сходимость ряда (1) к функции 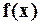в 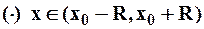означает, что:

или .

Теорема 1: Если функция 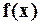имеет на интервале 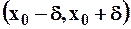производную любого порядка, ограниченную одним и тем же числом 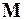, т.е. :

, то остаток ряда Тейлора стремится к нулю при 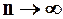, т.е. .

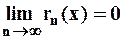Доказательство:

Теорема о представлении функции в виде формулы Тейлора (см. предыдущий семестр) гласит: если функция 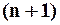раз дифференцируема в некоторой окрестности 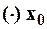, тогда такая что:

где 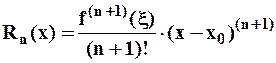– остаточный член в форме Лагранжа.

Итак, рассматривая остаток ряда Тейлора в виде остаточного члена в форме Лагранжа будем иметь:

, но при 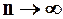правая часть последнего неравенства при любых конечных значениях .

Покажем справедливость последнего утверждения. Для чего рассмотрим следующий ряд: . Рассмотрим
,

т.е. данный ряд сходится для любых вещественных значениях . Но тогда по необходимому признаку сходимости ряда будем иметь:

для любого фиксированного значения . В нашем случае в качестве значения берётся значение .

Таким образом имеем, что при .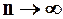

Итак, представление заданной функции 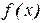в виде ряда Тейлора в окрестности 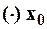состоит из двух этапов:

* Вычисление значений функции и её производных в 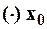и составление ряда Тейлора для функции 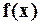. При этом полагается, что 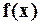– бесконечное число раз дифференцируема.

* Определение интервала, в котором составленный ряд Тейлора сходится к заданной функции 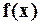, т.е. устанавливается, для каких значений 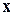остаток ряда .