ОПРЕДЕЛЕНИЕ РЯДА. СХОДИМОСТЬ И РАСХОДИМОСТЬ РЯДА.

Числовые ряды. Сходимость и сумма ряда. Необходимый признак сходимости. Знакопостоянные ряды. Достаточные признаки сходимости.

Ряды.

ЛЕКЦИЯ 1

 

Ранее были установлены свойства и правила при суммировании конечного числа слагаемых, например: сумма не изменяется при перестановке слагаемых, производная суммы функций равна сумме их производных и т.д. Вопрос состоит в том, что в каком случае м при каких условиях эти свойства конечных сумм могут переноситься на суммы бесконечные.

 

 

Пусть дана последовательность действительных чисел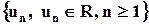

Выражение вида

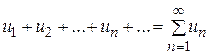(1.1)

называется числовым рядом, числа -членами ряда, 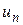- n-ым или общим членом ряда. Сумма n первых членов ряда называется n-ой частичной суммой и обозначается символом : .

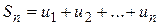Если для последовательности частичных сумм существует конечный предел S, то ряд (1.1) называется сходящимся, а число S –суммой данного ряда. В этом случае пишут: ; .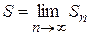

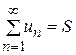Ряд (1.1) называется расходящимся, если 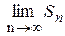не существует или бесконечен. Ряд, полученный из (1.1) отбрасыванием первых его m членов, называется остатком ряда (1.1):

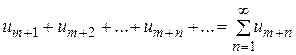(1.2)

Ряд сходится или расходится вместе со своим остатком.

Рассмотрим примеры.

Пример1: Пусть дана бесконечная последовательность 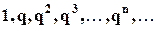. Рассмотрим ряд: 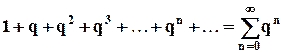. Его «n-ая» частичная сумма равна: 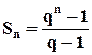. Рассмотрим случаи:

а) 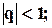найдём 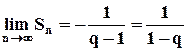, т.е. конечный предел существует и он равен конечному числу (сумма бесконечно убывающей геометрической прогрессии).

б) при этом: 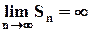и тогда ряд расходится.

в) Пусть 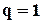. В этом случае ряд имеет вид: 1+1+1+…+1+… . При этом частичная сумма 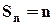и 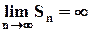. Значит ряд расходится (по определению).

г) Пусть 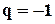. В этом случае ряд имеет вид: 1–1+1–1+1–… . При этом сумма 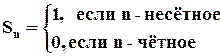, а тогда предел последовательности частичных сумм не существует и ряд не сходится. Т.о. имеем: исходный ряд сходится если 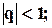и расходится, если .

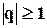Пример 2: Рассмотрим ряд: 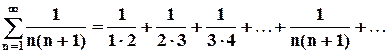. Заметим, что 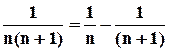. При этом n–ая частичная сумма ряда равна:

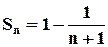и тогда 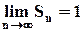. Таким образом, установили, что ряд сходится и сумма его равна 1.

Пример 3: Рассмотрим ряд: 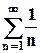. Рассмотрим частичные суммы ряда с номером :

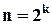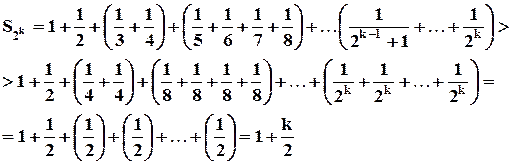
Т.о. имеем, что если 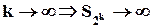, т.к. меньшая сумма стремится к бесконечности. Но мы рассмотрели только подпоследовательность последовательности частичных сумм. Последовательность 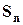является возрастающей последовательностью. Тогда и она будет стремиться к бесконечности, т.е. исходный (гармонический) ряд становится расходящимся.